化学自习室移动版

正四面体结构，只存在3个原子共面的情况。

普通四面体，可以存在最多3个原子共面，最少2个原子共面的情况。

首先，关于高中常见(或者说常规)有机物分子中有多少原子共面的问题，它的本质上可以理解为是一个微观层面的几何问题，核心是“旋转”和“排斥”二个方面。

复杂的、原子数目较多的有机分子，要更多考虑旋转！！！

简单有机分子，或者理解局部的分支，要更多考虑孤电子对的排斥作用！！！

对于数学较好的同学，或者说抽象思维能力较强的同学，又或者说空间想象能力强的同学，实际上这类共面或者共线的问题一点就透，因为这有点像在自己想象的空间里搭建积木的游戏，只不过这个积木是可以旋转的。

首先讲最简单的结构：

最多原子共面是一种特殊情况。

甲烷是一个稳定的正四面体结构，无论它怎么“旋转”，都只有3个原子共面，且四个氢原子完全对称，这个非常容易想象和理解，但是如果不是甲烷，而是其他有机分子，比如：

三氟甲基氯仿(CF₃Cl)的分子中，由于孤电子对的排斥作用，通常是碳原子和氯原子共面，而三个氟原子则位于与这个共面垂直的位置，三个氟原子共面。因此，三氟甲基氯仿最多也是三个原子共面。但因为孤电子对排斥，出现了“更少”的两个原子共面的场景。因此它有“最少”这一说。

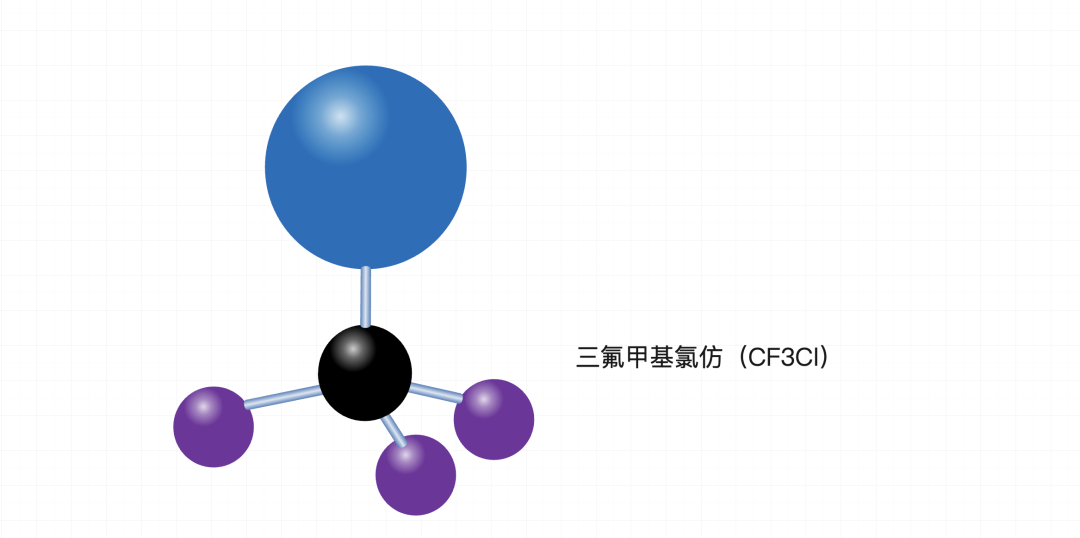
甲烷只有3个原子共面的情况，无论它怎么“旋转”，都是3个原子共面，不存在最多和最少的说法。

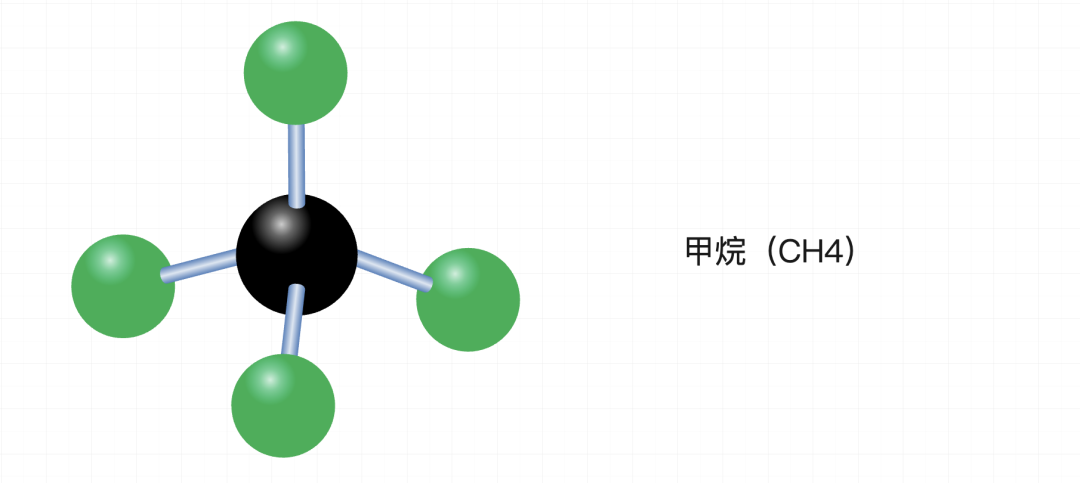
但是，当我们增加“孤电子对排斥理论”后，简单分子(Cf₃Cl)也可以出现“更少”的情况，这相当于回答了最少的原子共面情况。而相对复杂的分子，则可以通过“旋转”来改变自身结构中共面的原子数量。

再次强调一下：

对于简单的有机分子(四面体为例)，它已经简单到不能考虑旋转的思路来看待原子共面的问题时，要考虑孤电子对的排斥作用，翻译成更容易理解的语言就是观察它四个角位置的原子是不是一样的，一样的肯定就是正四面体，要是不完全一样(比如发生取代反应后)，就会存在不完全对称的情况(电子对偏移)，这个时候，分子结构就是一个非高度对称的四面体。

此时，分子依然满足最多有3个原子共面，但会出现最少有2个原子共面的情况。会让更少的共面情况出现。

举一反三一下，有没有可能出现更少的，一个原子共面的场景？

答案是不可能。因为我们但凡想象一下就可以发现，中心原子总能和某一个原子构成一条线，只要共线了，就必然共面，这意味着至少有2个原子共面。

讨论到这里，我们可以对四面体结构作出如下结论：

正四面体结构，只存在3个原子共面的情况。

普通四面体，可以存在最多3个原子共面，最少2个原子共面的情况。

对于常见的“可能共面”的问法：

碳碳双键、碳碳三键、碳氧双键、苯环均为平面结构，可能出现所有原子都共面的场景。

反观，但凡出现类似甲烷基本结构的化合物分子，则不可能出现所有原子都共面的场景。

【最多共面原子数】：

对于计算最多有多少个原子共面的问题，我们可以采取两条基本路线：

口诀，就是针对大部分题目的套路所总结的快速计算方法。

基本计算逻辑，主要是针对一些比较难计算的场景，当口诀不好用的时候，动用基本计算逻辑进行计算。

我们先讲基本计算逻辑，再说口诀。

【基本计算逻辑】：

出现类似甲烷的基本结构，看作甲烷的部分最多有3个原子共面。

出现类似乙烯的基本结构，看作乙烯的部分最多有6个原子共面。

出现类似乙炔的基本结构，看作乙炔的部分，4个原子均在同一条直线上（一定共面）。

出现含有苯环C6H6的基本结构，看作苯环的部分最多有6+6=12个原子共面，且对角原子共线。

【口诀】：

a 分析基本结构：转化成结构式比较方便看出对应的基本结构。

b 确认框架：确认基本结构是苯环、乙烯、乙炔还是别的。

c 遇到甲基，直接加1，遇到乙基，直接加2。

d 公式计算：最多共面原子个数 = (完整结构1的最多共面原子个数-N1)+(完整结构2的最多共面原子个数-N2)+······

其中的N1和N2指的是结构两端连接端量（有0、1、2三种情况）。比如乙烯是完整结构，最多6个原子共面，如果乙烯有2端连接了其他结构，这个连接端数就是2，要增加的原子数就是6-2=4。

我们来练习一下这个口诀如何快速解决问题。

练习一：CH₂CHCH₃最多有几个原子共面？

先写成结构式：

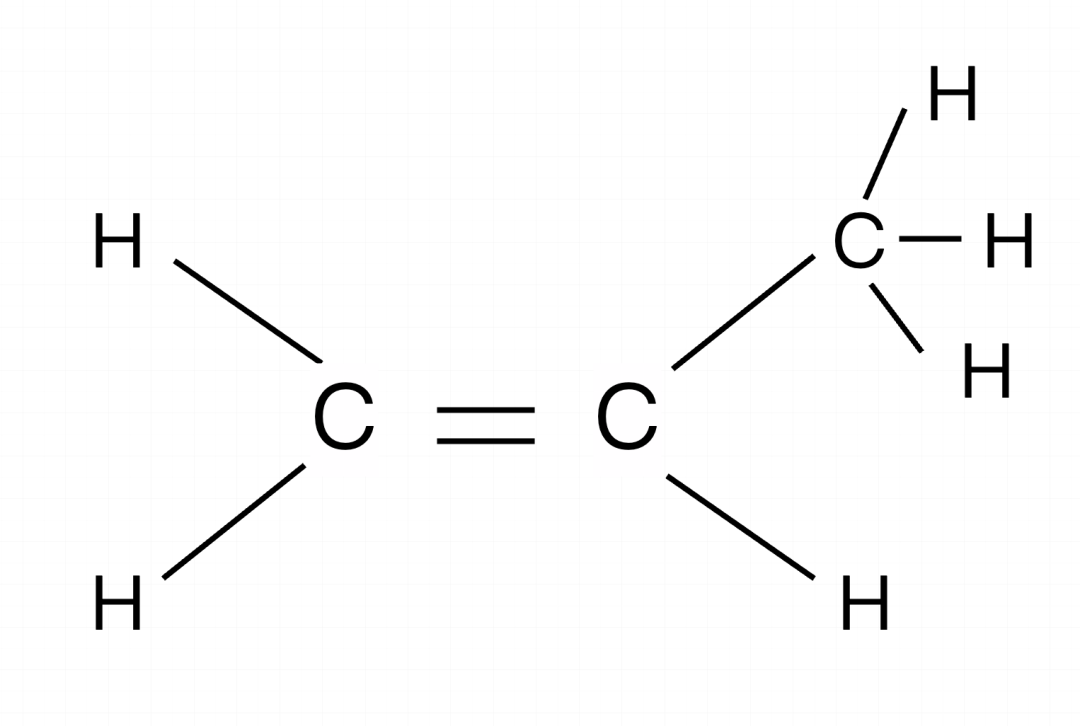
确认框架，有一个类似乙烯的结构（红色部分），有一个甲基（绿色部分）的结构，框架为乙烯，在乙烯的框架下进行计算。

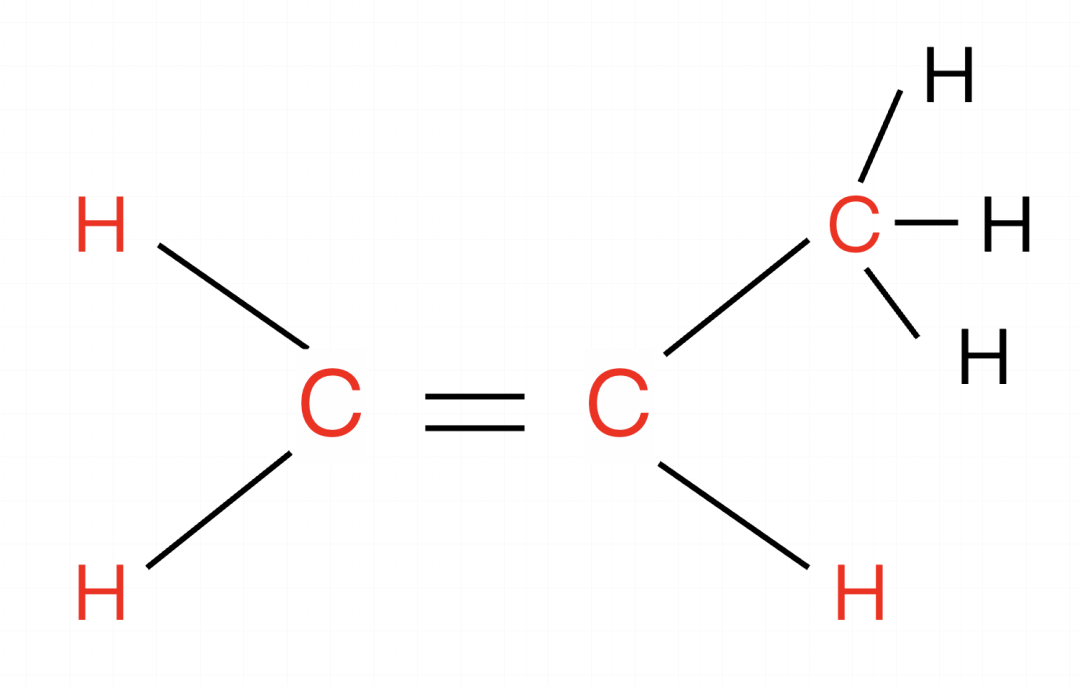
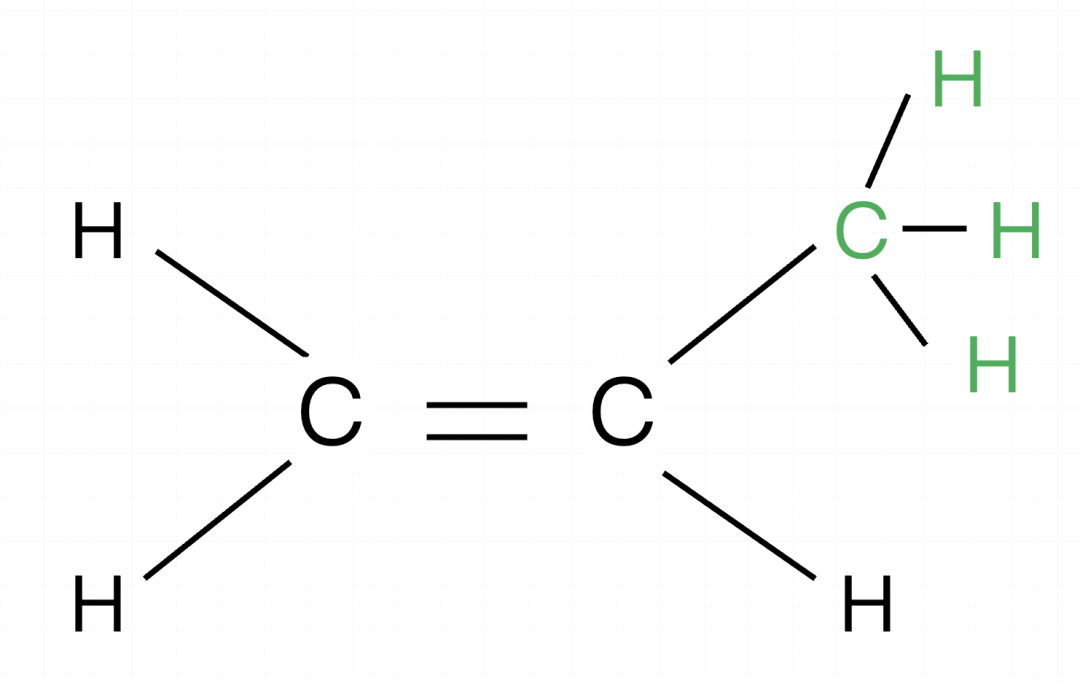
以乙烯为框架，这个分子结构相当于是完整的乙烯加一个甲基，乙烯是6个原子共面，遇到甲基直接加1，因此最多有(6-0)+1=7个原子共面。

练习二：以下分子中最多有多少原子共面？

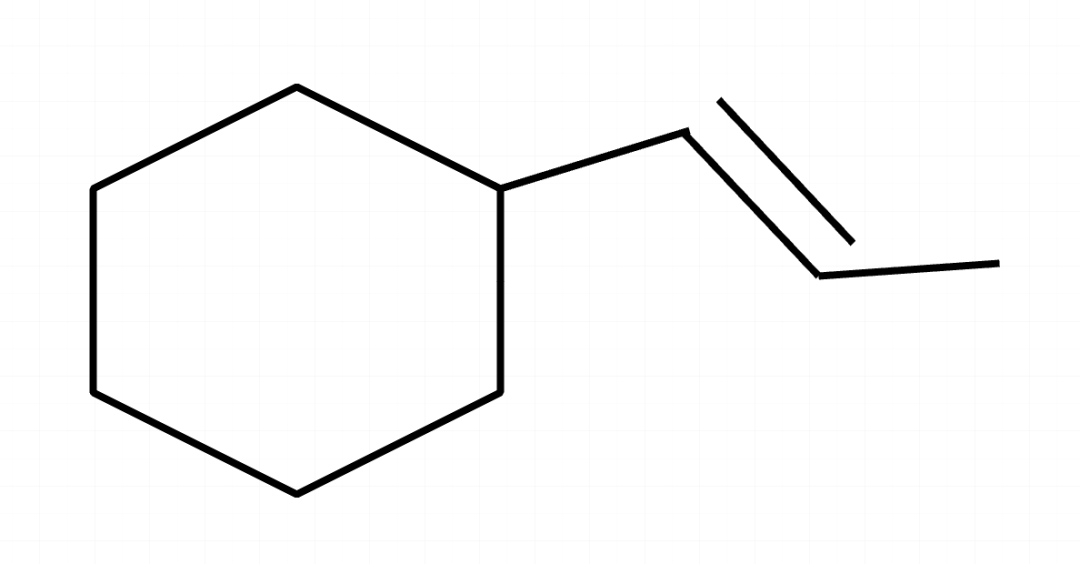
先转化成结构式：

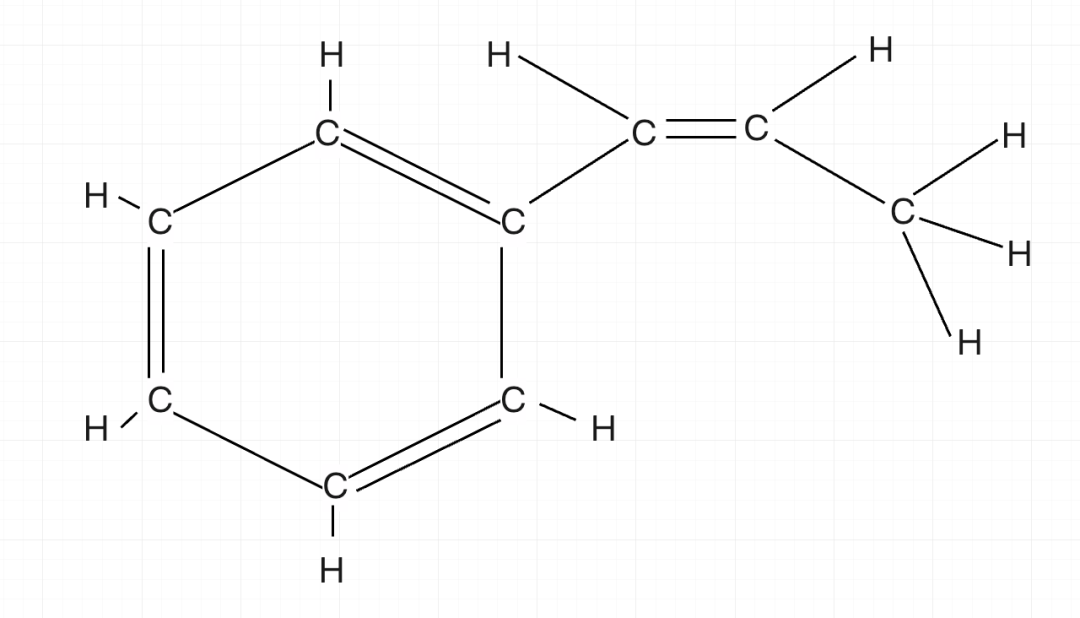
确认框架，有类似苯环的结构，肯定以一个完整的苯环为基准框架，然后有一个类似乙烯的框架，但这个乙烯相当于两端连接了其他部分，最后还加了一个甲基。

直接计算：(12-0)+(6-2)+1=17。

刚说到这个乙烯相当于前后都有连接，如果只有一个部分连接，那么我们怎么计算，那就相当于这个乙烯额外贡献了6-1=5个。

如果没有连接外部结构，可以看做一个完整的乙烯结构，那么贡献的共面原子就是6-0=6个。

【某部位最多共面原子个数计算规律】：

两头都接，对应结构完整数-2。

一头接，对应结构完整数-1。

不接，对应结构就是完整数。

【反思】——口诀的局限性。

首先，大家务必清楚一点，所谓的口诀都只是为了加快计算速度，它能解决很多问题，但绝对不是全部，因为问题的场景比较复杂，所以仅靠几个字的口诀就想解决浩如烟海的有机化学问题，无非是在做梦。

但是，我们还有另一个超级武器，就是基本计算逻辑。

画出对应的分子结构式，然后想象一下，分子机构通过旋转，被“按压”在一个平面或者“恰好”形成了一个平面，那么在这个神奇的时刻，原子个数是怎样计算的······

练习三：以下分子，最多有多少个原子共面？

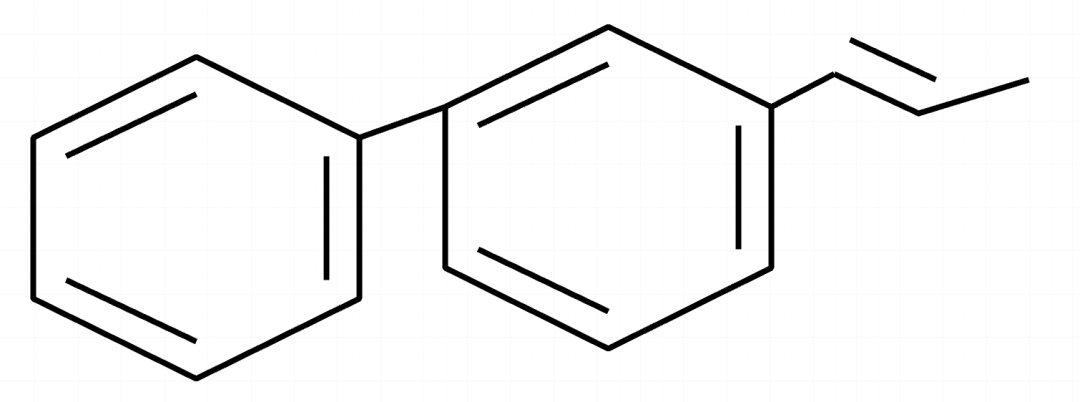
按照刚才的逻辑，我可以直接写出计算公式：

从左到右计算：(12-0)+(12-2)+(6-2)+1 = 27个

总结一下最少共面原子数需要用到的逻辑：

a 苯加炔，都共面

b 烯加炔，都共面

c 连接苯直接加2

d 甲基无视，加0

我们来练习一下这个口诀如何快速解决问题。

练习一：下列分子最少有几个原子共面？

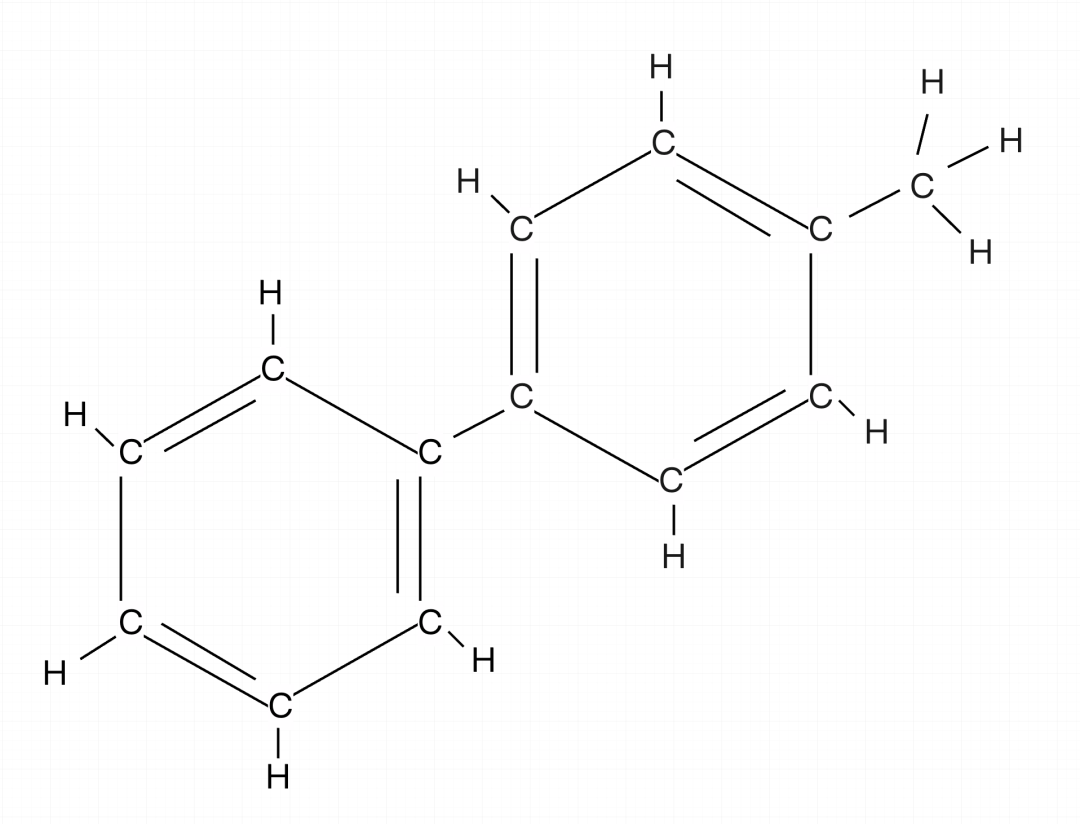
为了方便大家理解，直接给出了结构式。

这里可以给大家提供一个新的思路，就是我们在确认框架的时候，找连接最多的做为基准。在这个分子中，中间苯环连接基团最多，我们选取中间的苯环作为基准。

一个苯环有12个原子共面，中间苯环左下方又连接了一个苯环，所以再连接苯环直接加2，右上角连接了甲基，直接无视。最终的结果是12+2=14。以上的分子，最少有14个原子共面。

【为什么连接苯环要+2】：

理解角度：苯环对角线的原子不仅共面，而且共线，可以理解为最少共面就是共线。苯环对角线上正常是4个原子，一个是C+H，另一个也是C+H，但是苯环一旦连接，H的位置往往被占用了。

我们在数中间苯环的12个原子时（绿色部分），实际上把左下方苯环和中间苯环连接的C原子也计入了12的名额，因此对角线只剩下了和C原子对角的C—H组合的2个（红色部分），因此是连接苯环再加2。

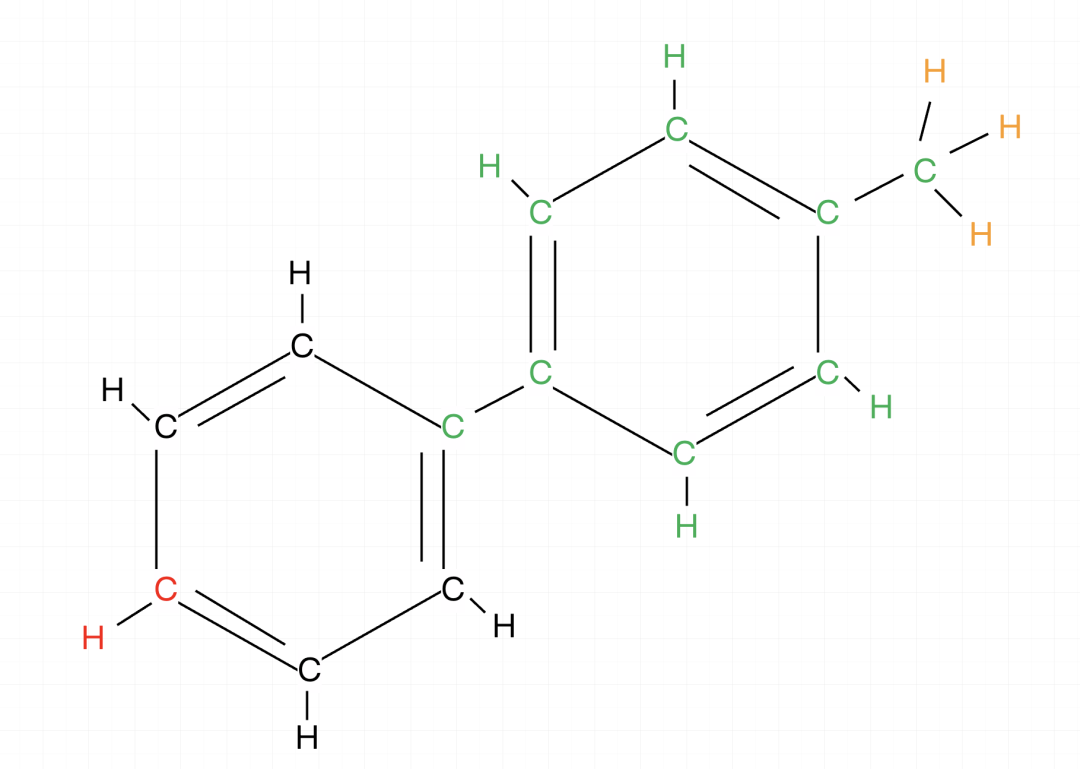
【甲基为什么无视】：

甲基含有一个C原子，但是这个C原子往往被记入别的结构里了，剩下的三个氢原子可以通过旋转实现不和C原子共面的情况。或者说，C原子通过和连接前面部分的单键旋转，把自己转出原来的平面。我们考虑的是最少原子共面的情况，当然可以是0。

练习二：以下分子中最少有多少原子共面？

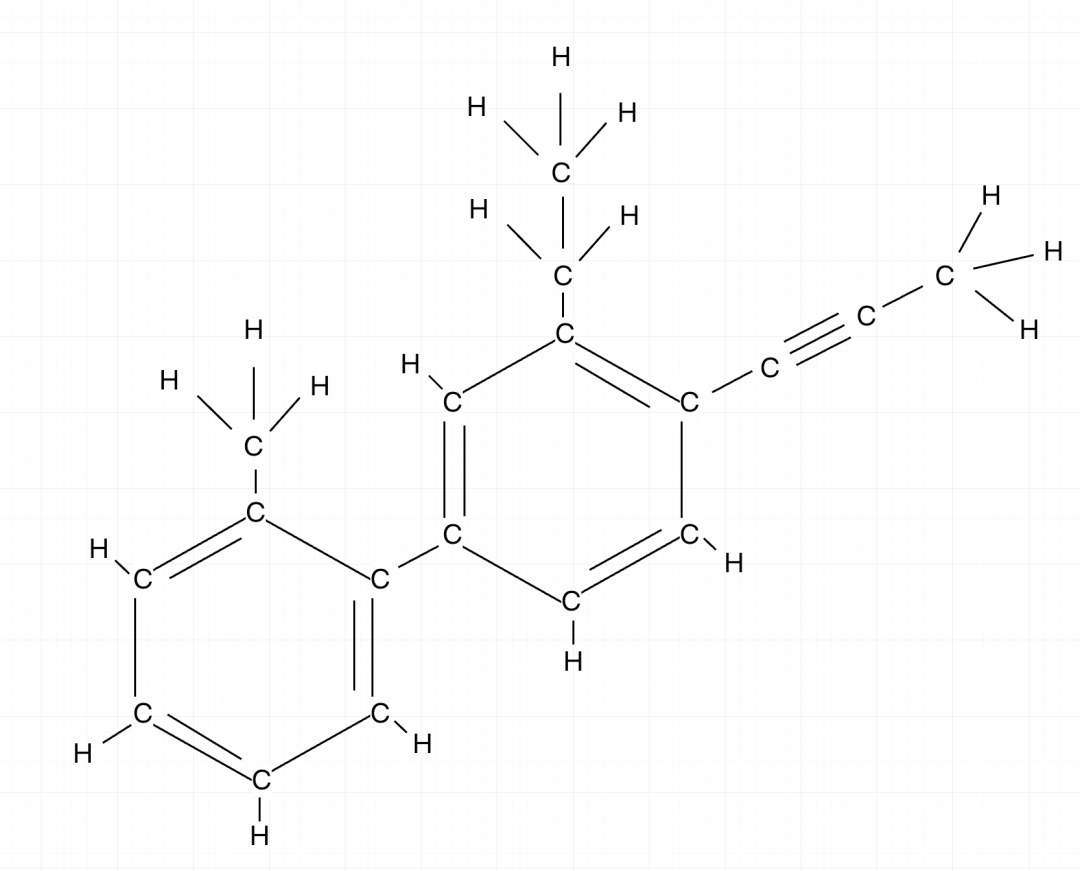
确认框架，中间的苯环连接有最多的基团，以中间苯环为基准，把乙炔也记入，因为苯环连接乙炔，二者一定都共面，画出二者的结构范围（红色部分）。

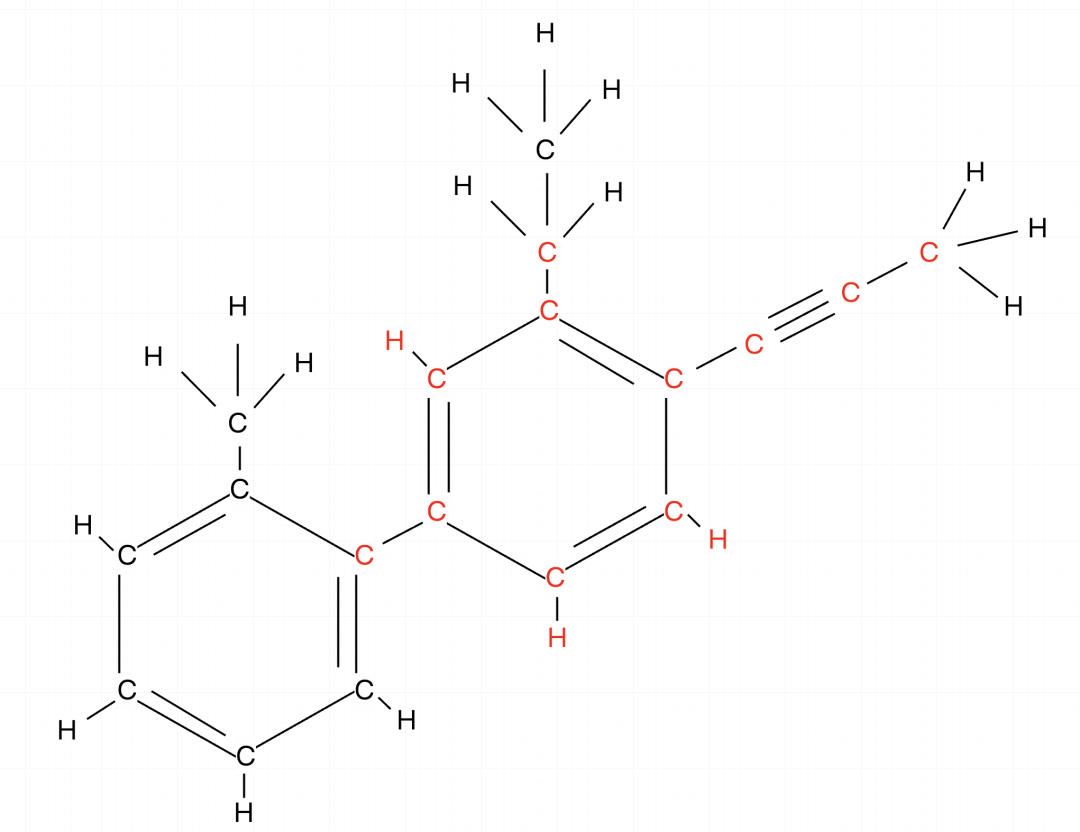
红色范围内一共有14个原子。

左下方还连接有一个苯环，连接苯环再加2（蓝色部分）。

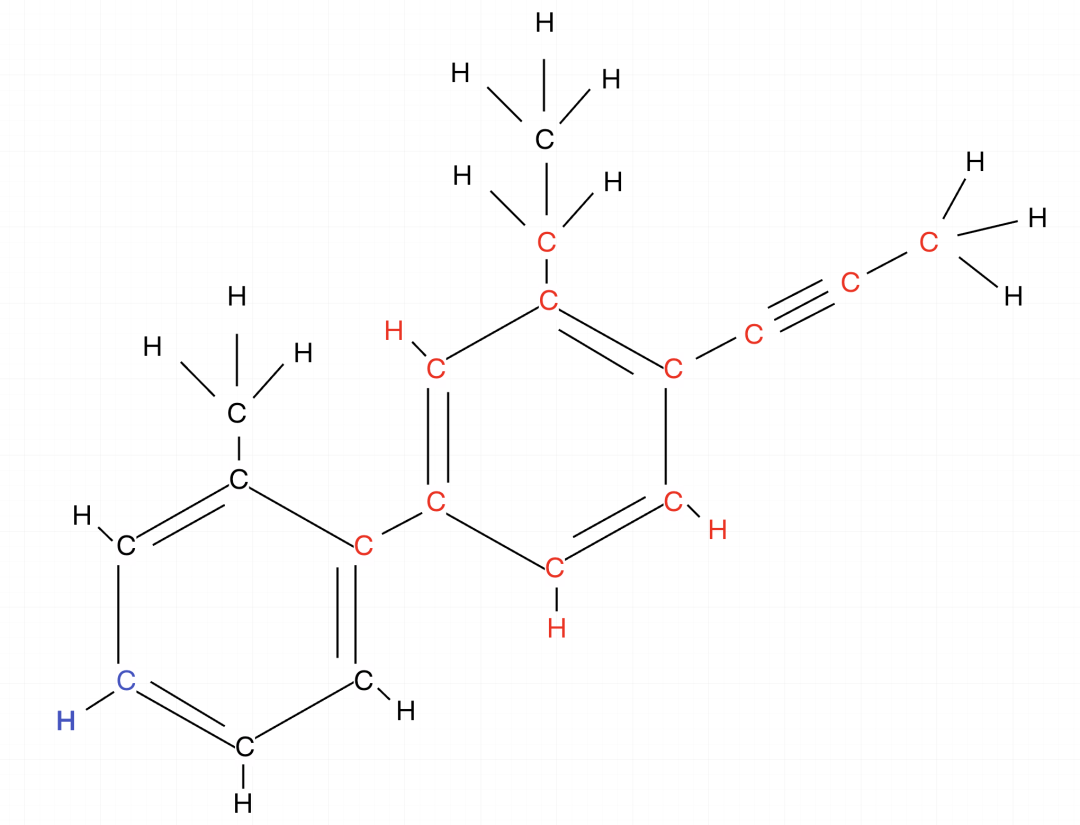
14+2=16，截至目前最少有16个原子共面。

其余部分是甲基，甲基无视，不用加。

因此结果就是最少有16个原子共面。

【一定共线】：

a 乙炔所有原子一定共线。

b 苯环的对角线原子一定共线。

c 连接苯环+2。

下面借助练习来理解逻辑。

【练习】以下分子中，有多少个原子一定共面？

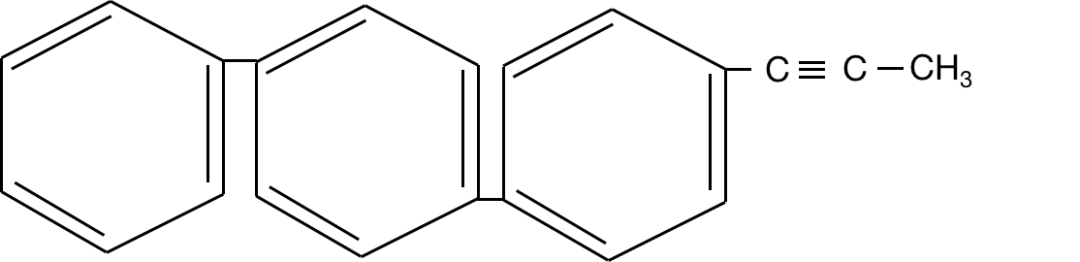
这个结构其实给的已经比较具体和形象了，但是我们可以把它处理地再形象、再容易理解一些。如下图：

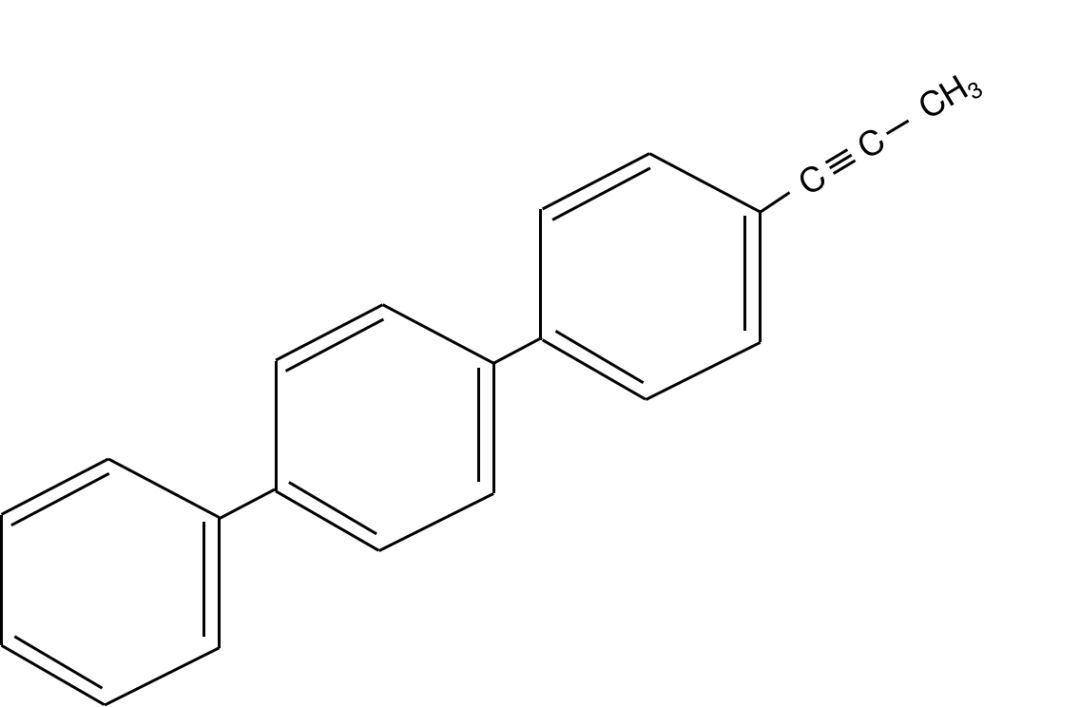
处理成这个样子后，我相信已经很好判断了。乙炔所有的原子本来就是共线的，对苯环而言，只有对角线的部分一定共线。

可以想象一下，三个大苯环，围绕中间那条轴线旋转。

还是从最上面的苯环作为基准开始计数（因为这个苯环所连接的基团最多最复杂）。

由于问题问的是一定共线，而苯环中一定共线的是对角线的原子，所以是4个（红色部分，先把4个占上）。

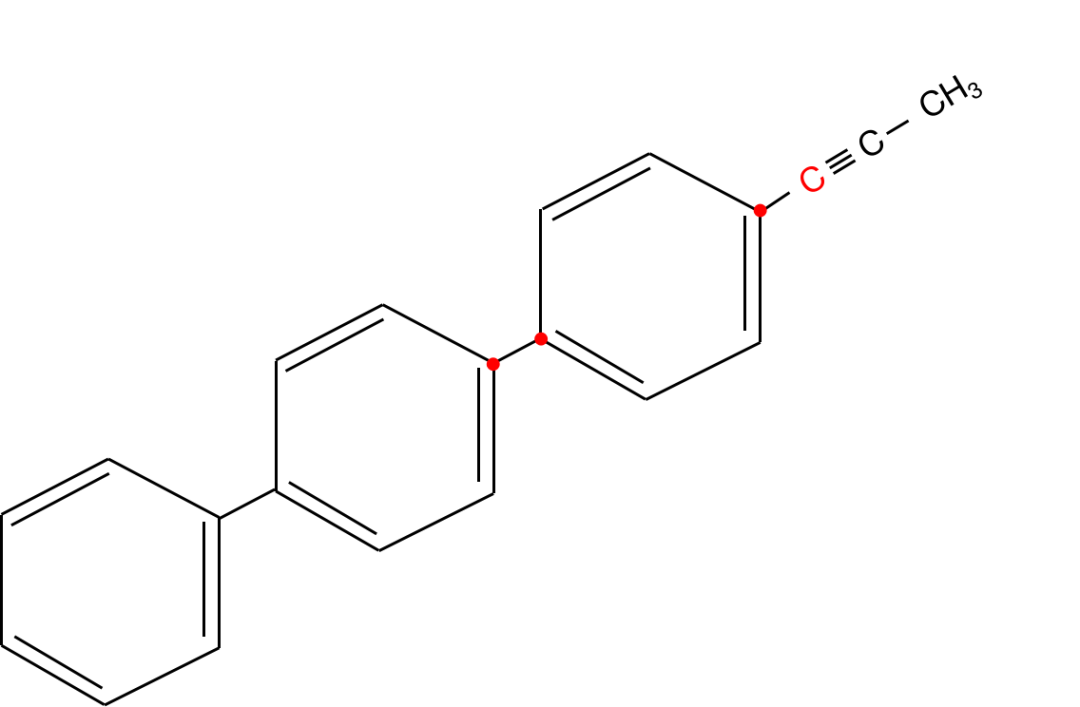
然后计算乙炔一定共线的部分。额外增加了2个（紫色部分）。

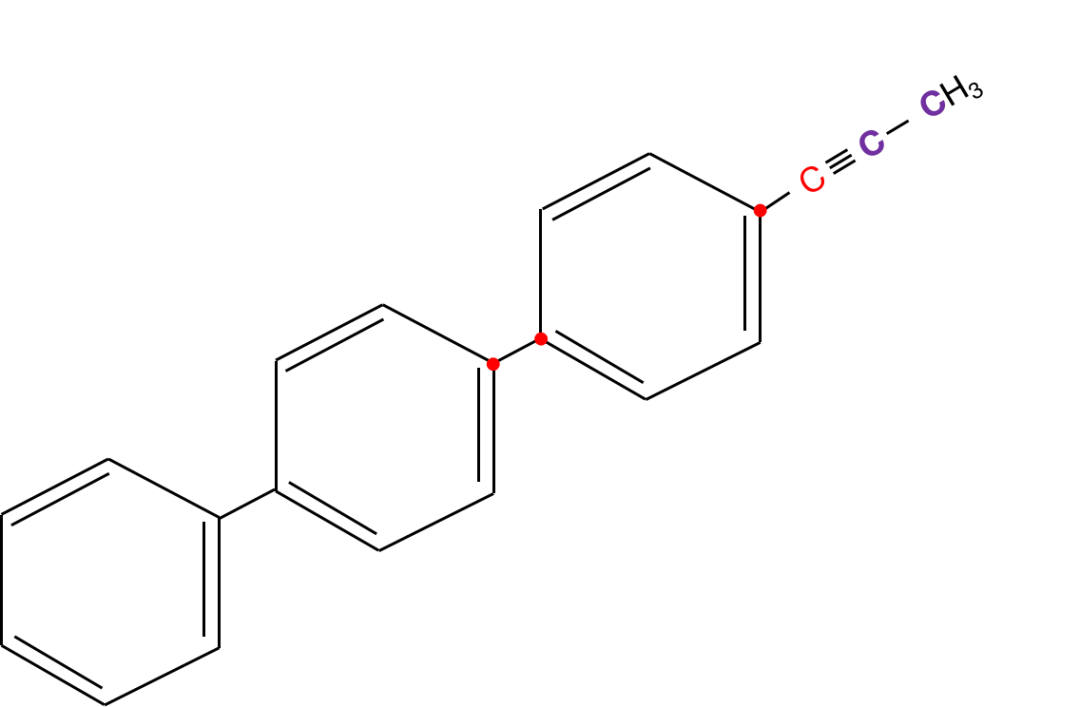
目前有4+2=6个原子一定共线。

继续计算苯环的部分。

连接苯环就+2，左下方连接了2个苯环，所以是2+2=4。

总共一定共线的原子数为6+4=10。

右上角是个甲基，甲基里都是C-H单键可以旋转，不一定共线。

因此，这个有机分子一定共线的原子数为10个。