化学自习室移动版

由于其他电子对某一电子的排斥作用而抵消了一部分核电荷，从而引起有效核电荷的降低，削弱了核电荷对该电子的吸引，这种作用称为屏蔽作用或屏蔽效应。因此，对于多电子原子来说，如果考虑到屏蔽效应，则每一个电子的能量应为：E＝－13.6×(Z－σ)²/n²(eV)，其中Z为原子序数，n为主量子数，σ为屏蔽常数。E值越大，则说明电子能量越高。从式中可见，如果能知道屏蔽常数σ，则可求得多电子原子中各能级的近似能量。影响屏蔽常数大小的因素很多，除了与屏蔽电子的数目和它所处原子轨道的大小和形状有关以外，还与被屏蔽电子离核的远近和运动状态有关σ屏蔽常数。可用斯莱脱提出的计算屏蔽常数的规则求得。

斯莱脱规则如下：将原子中的电子分成如下几组：(1s) (2s，2p) (3s，3p) (3d) (4s，4p) (4d) (4f) (5s，5p)，如此类推。

①位于被屏蔽电子右边的各组，对被屏蔽电子的σ＝0近似的可认为：外层电子对内层电子没有屏蔽作用。

②1s轨道上两个电子之间σ＝0.30。其他主量子数相同的各分层电子之间的σ＝0.35。

③当被屏蔽电子为ns或np时，则主量子数为(n－1)的各电子对它们的σ＝0.85，而小于(n－1)的各电子对它们的屏蔽常数σ＝1.00。

④被屏蔽电子为nd或nf电子时，则位于它左边各组电子对它们的屏蔽常数σ＝1.00。

在计算某原子中某个电子的σ值时，可将有关屏蔽电子对该电子的σ值相加而得。

K：（1s²）（2s²2p⁶）（3s²3p⁶）（3d⁰）（4s¹  ）  Sc：（1s²）（2s²2p⁶）（3s²3p⁶）（3d¹）（4s²)

如，19号K原子的价电子是3d¹还是4s¹，可以通过该公式计算并进行判断。如果是3d¹，则σ=18×1.00=18.00，E(3d)=－1.51eV ；而如果是4s¹的话，则σ=8×0.85+10×1=16.8 ，E(4s)=－4.11eV 。E(3d)＞E(4s)，所以价电子填充在4s轨道上，更符合能量最低原理。

再如，21号Sc原子的价电子为3d¹4s²，也可以通过计算比较3d和4s轨道上电子的能量高低。在3d中，σ=18×1.00=18.00 ，E(3d)=－13.6eV，而4s中,σ=18×1.00=18.00，E(4s)=－7.65eV 。E(3d)＜E(4s)，所以能量高的4s电子首先失去。

通过对第四周期元素3d和4s轨道能量的计算(见表1)，可以发现只有K、Ca：E(3d)＞E(4s)；而其他元素原子均呈现E(3d)＜E(4s)

表1 第四周期元素原子3d、4s轨道上电子的能量

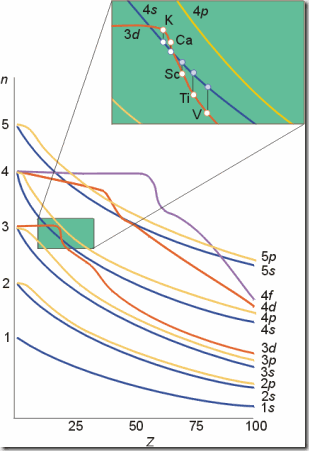
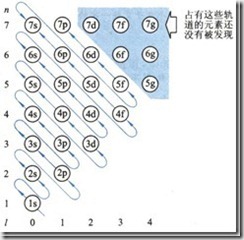
Cotton能级图                                                               Pauling近似轨道能级图

 我们在填充电子的时候，使用了一个工具，在选修3将它称为“构造原理示意图”，其实它的准确名称应该是“Pauling近似轨道能级图”，在进行教学时，学生容易“错误”的理解填充的顺序一定是按照能量由高到低进行的。其实这一图形之所以是“近似”的，就是由于它没有考虑能级的能量还要受到核电荷数的影响，Cotton为了解决这一问题，通过光谱数据和理论计算绘制了更为准确的“Cotton能级图”。

取出Cotton能级图局部，可以看出当开始填充3d轨道后，4s能级的能量便下降至：E_4s<E_3d，所以26号Fe失去能量更高的4s电子并不超出我们的理解。

关于第四周期开头的元素 K, Ca, Sc, Ti 的最后几个电子的填充,由体系的总能量的降低程度决定, 而且, 原子的总能量不仅仅取决于某个原子轨道的能量, 尚有其它能量形式存在. 先填充哪个轨道也取决于是否使体系更加稳定.普遍认为:

1) 填充电子时, 为离子状态, Z*比原子状态的大, 体系不同

2) 先在4s上填充电子, 比先填入3d稳定, 因为4s的钻穿能力比3d大, 使电子更加靠近核,整个体系能量降低幅度大.

＊Slater规则的不足之处: (nsnp)同组, 无法区分它们能量的高低.

＊Pauling 近似能级图不足之处:无法反映轨道能量随与原子序数增加而下降的规律.

二者相辅相成, 各得益彰