化学自习室移动版

所谓密堆积原理是指由无方向性的金属键、离子键和范德华力等结合的晶体中，原子、离子和分子等微粒总是趋向于相互配位数高，堆积密度大，能充分利用空间，因而体系稳定的那些结构。金属原子的电子云分布基本上是球对称的，可以把同一种金属晶体看成是由半径相等的圆球构成，因此金属晶体的结构可用等径圆球的密堆积模型来研究。常见的堆积形式有：A1、A2、A3和A4等。

A1（立方最密堆积，ccp，记为 A1型）和A3（六方最密堆积，hcp，记为A3型）堆积是等径球的密置层以两种不同方式堆积而成的最密堆积。

如图所示，每个球与6个球紧密接触，形成6个三角形空隙，其中1、3、5三角形空隙的底边在下、顶点在上，2、4、6三角形空隙的底边在上、顶点在下。

在堆积第二层等径球时，这个密置层中圆球的凸出部位正好处于第一密置层的凹陷部位，也就是一个球同时与第一密置层的三个球接触，它可以占据1、3、5空隙，也可占据2、4、6空隙，但不会两者都占，也不会混合占据。如果占据1、3、5空隙，第一密置层中的1、3、5三角形空隙转化成密置双层中的底面在下、顶点在上的正四面体空隙T+，见图（a）。而2、4、6三角形空隙转化成正八面体空隙O，见图（c）。注意在7位还有一个底面在上、顶点在下的正四面体空隙T-，见图（b）。

两个密置层间形成的空隙种类及分布下图所示。

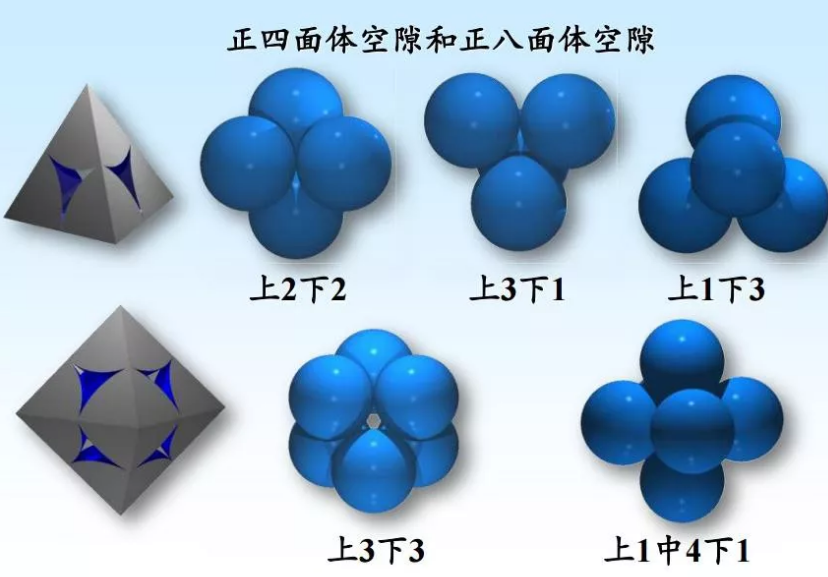
在这两种堆积方式中，任何四个相切的球围成一个正四面体空隙；另外，相切的三个球如果与另一密置层相切的三个球空隙对应，它们六个球将围成一个正八面体空隙。

也就是说，围成正八面体空隙的这六个球可以分为相邻的两层，每层的正三角形中心的连线垂直于正三角形所在的密置层，参看下图，黑色代表的不是球而是正八面体的中心。

在这两种最密堆积方式中，每个球与同一密置层的六个球相切，同时与上一层的三个球和下一层的三个球相切，即每个球与周围十二个球相切（配位数为12）。中心这个球与周围的球围出八个正四面体空隙，平均分摊到每个正四面体空隙的是八分之一个球。这样，每个正四面体空隙分摊到的球数是四个八分之一，即半个。中心这个球周围还围出六个八面体空隙，它平均分摊到每个正八面体空隙的是六分之一个球。这样，每个正八面体空隙分摊到的球数是六个六分之一，即一个。总之，这两种最密堆积中，球数 : 正八面体空隙数 : 正四面体空隙数 = 1:1:2 。