化学自习室移动版

等径球最密堆积中的空隙分两种:

(1)四面体空隙:由四个球体围成的空隙，球体中心线围成四面体;

(2)八面体空隙:由六个球围成的空隙，球体中心线围成八面体形。

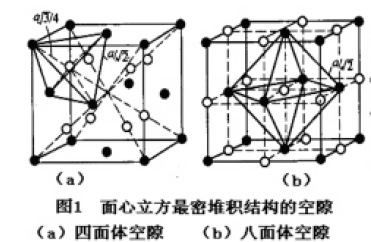
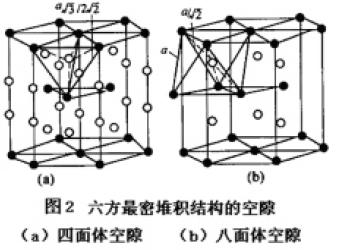
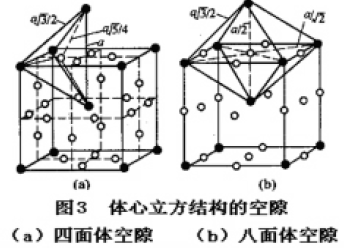
面心立方最密堆积结构中的空隙如图1所示，六方最密堆积结构的空隙如图2所示，体心立方堆积结构的空隙如图3所示。

以金属Cu晶胞为例，来说明面心立方紧密堆积中的八面体和四面体空隙的位置和数量:

以Cu晶胞中上面心的一个球为研究对象，它的正下方有1个八面体空隙(体心位置)。与其对称，正上方也有1个八面体空隙;前后左右各有1个八面体空隙(棱心位置)。所以一个球共参与形成了6个八面体空隙，由于每个八面体空隙由6个球构成，所以属于这个球的八面体空隙数为6×1/6=1。

在这个晶胞中，上面心这个球还与另外两个相邻面面心处的2个球及顶角上的1个球，共能构成4个四面体空隙(即1/8小立方体的体心位置);由于对称性，在上面的晶胞中，也有4个四面体空隙由这个球参与构成。

所以一个球共参与形成了了8个四面体空隙，由于每个四面体空隙由4个球构成，所以属于这个球的四面体空隙数为8×1/4=2。

因此，我们不难证明:对有n个等径球体紧密堆积而成的系统中，共有:四面体空隙=2n个(除以4原因是四面体空隙由四球围成);八面体空隙=n个(除以6原因是八面体空隙由六球围成)。

那么，四面体和八面体空隙中可填充原子的半径是多大呢?这个可以借助立体几何知识解决:

四个等径球围成的正四面体空隙所能填充的球体半径恰好就是四面体中心到顶点的距离与球体半径之差。若四个等径球半径为R，则中心到顶点的距离为，可得正四面体空隙所能填充的球体半径为。六个等径球围成的正八面体空隙所能填充的球体半径恰好也是八面体中心到顶点的距离与球体半径之差。若六个等径球半径为R，则中心到顶点的距离为，可得正八面体空隙所能填充的球体半径为。有了这些知识储备就可以解决一些原子堆积中的空隙填充问题。

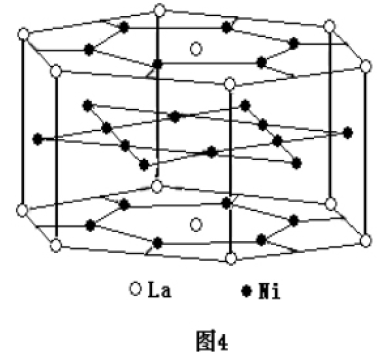
如氢是重要而洁净的能源。要利用氢气作能源，必须解决好安全有效地储存氢气问题。化学家研究出利用合金储存氢气，LaNi₅是储氢材料，它是六方最密堆积，晶胞体积为90×10^－24cm³，若晶胞所有的八面体空隙和四面体空隙，全部都填上氢原子，问此合金的化学式可以写为               ，该储氢材料吸氢后氢的密度为               。计算，该密度是标准状态下氢气密度(8．987×10^－5g/m³)的倍?(氢的相对原子质量为1．008;忽略吸氢前后晶胞的体积变化)。