学法指导:如何进行高考化学计算总复习
时间:2020-03-05 12:44 来源: 作者:陈爱玉 点击: 次 所属专题: 化学计算
版权申明:凡是署名为“化学自习室”,意味着未能联系到原作者,请原作者看到后与我联系(邮箱:79248376@qq.com)!
化学计算是高考中一个非常重要的考点,它贯穿在化学的基本概念、基础理论、元素及其化合物、化学实验等多方面的知识中。根据近几年高考化学计算的命题趋向:注重原理与性质的结合,强调从定量的角度分析题意简化计算;注重与生产生活实际的结合以及与新信息的结合,采取分层设问,考察不同知识层次;注重一题多解及开放性试题。在化学计算的复习中,应该主张“分散难点——集中总结”的复习思路,下面就谈谈本人的粗浅的看法。
一、分散难点,计算渗透各板块
在第一轮复习中必须纵观全局,注意各章节计算内容的合理渗透,循序渐进打好扎实的计算基础。计算的最大特点就是较枯燥,理论性、逻辑性较强,学生在复习过程中很容易感到厌烦,因此,在复习过程中,应分散难点,把有关化学计算的内容分散到各知识板块中复习。根据近几年高考中出现的计算类型,总结如下:
1、有关相对原子质量、相对分子质量及确定化学式的计算。
2、有关物质的量的计算。
3、有关气体摩尔体积的计算。
4、有关氧化还原反应的计算
5、有关化学方程式的计算。
6、有关物质溶解度的计算。
7、有关溶液浓度(溶质质量分数和物质的量浓度)的计算。
8、有关溶液PH值与氢离子浓度、氢氧根离子浓度的简单计算。
9、有关反应速率和化学平衡的计算。
10、有关原电池、电解电镀的计算。
11、有关热化学方程式的计算。
12、有关过量的计算。
13、有关混合物的计算。
14、各类计算类型的综合计算。
在复习过程中,将以上计算类型分散到各个知识板块中复习,具体做法是:
1、把以物质的量为中心的计算放在基本概念中复习,因为在复习原子量、物质的量、气体摩尔体积、物质的量浓度等概念时,必将牵连到有关基本计算,这些既是基本概念的内容,又是化学计算的必不可少的计算工具,所以将其放在基本概念中复习。再如有关溶解度的计算,因学生是在初三时学习溶解度的,并且他们在学习溶解度时要求也不是很高,只要会进行较简单的计算即可,而在高考中关于溶解度的计算要求就比较高,所以在复习时难度也不宜一下子提得太高,总要让学生有一个循序渐进,逐步适应的过程,因此,也把溶解度的计算放在基本概念中复习。
2、化学反应速率、化学平衡的有关计算是复习过程中最大的难点,化学反应速率及化学平衡的理论的抽象性以及逻辑性本来就很难讲解,加上它条件的多样性,使其成为学生较难掌握的一种计算类型。所以在复习中将本部分内容穿插在基本理论的复习中,使学生在理解理论的基础上解答有关的计算。
3、有关PH值的计算和电解电镀的计算则归类在电解质溶液的复习中。关于PH值的计算在高考中要求不是很高,只要掌握简单的计算即可。电解电镀的计算是建立在充分理解电解原理的基础上,并能熟练应用电解反应中电子守恒这一原理来解答相关的计算。所以掌握好这两类计算并不是很难,重点在于理解其原理。
4、在复习元素化合物中的氮族时则穿插过量计算的复习,介绍过量计算的常见题型及解题思路的分析。过量计算的题型往往较灵活,在复习中应该在解题思路的培养上下工夫。在硫酸和硝酸的工业制法中穿插连续反应的计算和关系式法的应用,因为工业制硫酸和硝酸都是连续反应,若按化学方程式来进行计算,步骤烦琐又容易出错,但可用关系式法来进行计算,既简洁明了,又不容易出错,是解连续反应的常用方法。在碱金属的复习中穿插有关混合物的计算,因在这里常常出现碳酸钠和碳酸氢钠混合物的计算。
二、专题训练,总结归纳
在第二轮化学计算的板块复习中将以上各个分散复习的计算类型、方法进行整合、归类,形成网络结构,力求能使学生站在一个较高层次上纵观整个化学计算复习的过程。在复习过程中,有关计算方法的复习也是非常重要的,化学计算技法是解题的钥匙,掌握好这些方法无疑对化学计算有很大的帮助,起到事半功倍的效果,当然这些方法不是孤立的,不可交叉的,在解题过程中,往往应用到多种方法和技巧,只要熟练掌握这些技巧,并加以适当的练习,就能在解题中融会贯通、快速解答。因此,在第二轮复习中将主要的计算方法列为专题来复习。共分十个专题,重点放在解题思路分析和计算技能、技巧的讨论上,培养学生的思维能力,提高复习效益。
1、关系式法——多步变化以物质的量关系首尾列式计算。
2、差量法——根据变化前后的差量列比例计算。
3、守恒法——运用质量、元素、得失电子、电荷守恒计算。
4、参照法——对没有或缺少数据的题目参照化学原理等计算。
5、估算法——避开烦琐解题寻找快速方法解题。
6、信息转换法——为解题寻找另一条捷径。
7、极值法——对数据处理推向极端的计算。
8、平均值法——求平均相对原子质量、平均相对分子质量、平均分子式的主要方法。
9、数轴法——多步反应中取值范围讨论的计算
10、十字交叉法——对于二元混合物问题运用交叉法。
下面略举几例:
(1)信息转换法(由一般转化为特殊)
有些化学计算题若从一般情况考虑,思路不畅,计算繁杂。此时不妨从特例入手,使抽象问题具体化,从而达到简化计算、迅速求解的目的。
例:在化合物X2Y和YZ2中,Y的质量分数分别为40%和50%,则在化合物X2YZ3中,Y的质量分数是多少?
分析:根据Y在化合物X2Y和YZ2中的质量分数,虽能求得Y在X2YZ3中的质量分数,但难度大,技巧性高,稍不留神,往往半途而废。若根据Y在X2Y中的质量分数,假设Y的原子量为40(化一般为特殊),由题意得X
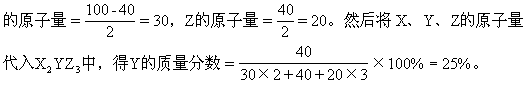
(2)参照法
有些题目从表面看来似缺条件而无法求解,实际上解题条件就隐含在语言叙述、化学现象、化学原理之中。解答此类题目的关键,是充分挖掘题中的隐含条件,化隐为显,架设由未知到已知的“桥梁”。
例:.将镁粉和碳酸镁的混合物置于氧气中灼烧,直至质量不再改变为止。经测定,灼烧后所得固体质量与原混合物质量相同,求原混合物中镁粉和碳酸镁的质量比。
分析:整个题目全用文字叙述,没有一个可供直接利用的具体数据。仔细审视题意,抓住关键词语,将“灼烧后所得固体质量与原混合物质量相同”转化为(化隐含为显露)“Mg吸收的O2质量等于MgCO3分解放出的CO2质量”,即可由2Mg~O2和MgCO3~CO2,导出44Mg~16MgCO3。这一关系式表明,在原混合物中镁粉与碳酸镁的质量比是44×24∶16×84=11∶14。
(3)估算法
有些化学计算题表面看起来似乎需要进行计算,才能求得结果,但只要稍加分析,严谨审题,就可以很容易得到正确结果,从而省去了许多烦琐的计算,提高了解题速度。此方法适合解选择题和填空题。
例:密度为0.91g·cm―3的氨水,质量分数为0.25,该氨水用等体积的水稀释后,所得溶液的质量分数为( )
A 12.5% B 13.1% C 11.9% D无法确定
解析:本题按通常的算法,先设各用1L溶液混合,按
NH3%(稀)= | 原氨水1L中氨的质量 原氨水1L的质量+1L水的质量 | ×100% |
进行计算,原理简单,但运算烦琐。若从题给选项0.25/2=0.125(即12.5%)为基准进行分析,由于稀释时所加水的密度>氨水的密度,所以稀释后溶液质量不只扩大了一倍,即上述公式中分母增大了一倍多而分子不变,所得的商肯定小于原值的1/2。因此,稀释溶液的浓度<12.5%。故选C
另外,这里值得提一下的是关于计算型选择题的解法:根据计算型选择题“只要结果,不要过程”的特点,指导学生注意从题干上抓信息,从备选答案中找启示,从定量关系上作判断,从限制条件中寻答案,要能自觉运用估算、守恒法、差量法、平均值法、十字交叉法去巧解速算。

- 全部评论(0)
