化学自习室移动版

晶体的有关计算是高考的热点，又是教学的难点。本文利用晶体的数学模型，构建宏观体积、质量、密度与微观粒子的数目、占有的体积、质量等的关系及确定晶胞所拥有的原子数。深入认识和准确把握晶体的特点。

[例1] 　食盐晶体是由钠离子和氯离子组成的，且均为等距离的交错排列。已知食盐的密度是2.2g/cm³，阿伏加德罗常数为6.02×10²³mol^-1。在食盐晶体中两个距离最近的钠离子中心间的距离最接近于(　　)。

A.3.0×10^－8cm B.3.5×10^－8cm C.4.0×10^－8cm  D.5.0×10^－8cm

解：根据均摊原则计算一个晶胞拥有的离子数：１.立方体中处于顶点的粒子，同时为８个晶胞所共有，每个粒子有1/8属于该晶胞；2.处于棱上的粒子，同时为4个晶胞所共有，每个粒子有1/4属于该晶胞；3.处于表面上的粒子，同时为2个晶胞所共有，每个粒子有1/2属于该晶胞；4.处于该晶胞内部的粒子，则完全属于该晶胞。

由此计算，在一个氯化钠晶胞中，拥有4个钠离子和4个氯离子。

如右图，设该晶胞的边长为A，两个距离最近的钠离子中心间的距离为B，则

方法一：依据1mol 氯化钠固体的体积建立等量关系式。

1mol 氯化钠的质量为58.5g，由密度得体积为58.5g/2.2g·cm³，1mol 氯化钠含有的晶胞数为N_A/4，一个晶胞的体积是a³，故1mol 氯化钠的体积是N_A·a³/ 4。即：

58.5g/2.2g·cm³=N_A·a³/ 4

a=5.6×10^－8 cm

b=a/2=4.0×10^－8cm

方法二：依据1个氯化钠晶胞的质量建立等量关系式。

58.5g×4/ N_A=2.2g·cm³·a³

a=5.6×10^－8cm

b=a/2=4.0×10^－8cm

方法三：依据1mol 氯化钠固体的密度建立等量关系式。

2.2g·cm³=58.5g×4 / N_A a³

a=5.6×10^－8cm

b=a/2=4.0×10^－8cm

此题关键是掌握体积、密度、质量与物质的量、微粒数之间的计算关系。从不同的角度认识同一问题，有利于深化理解，灵活运用。

[例2]最近发现一种钛原子和碳原子构成的气态团簇分子，如图所示，顶角和面心的原子是钛原子，棱的中心和体心的原子是碳原子，它的化学式为             。

[解] 由于钛原子和碳原子构成的是单个气态团簇分子，是分子晶体，边界原子不会分摊，都属该分子拥有，故它的化学式为Ti₁₄C₁₃。

很多同学不注意审题，以为与氯化钠离子晶体相似，结果计算出Ti₄C₄的错误结果。

[例3] 石墨的结构如课本所示，已知石墨的密度2.22g/cm³，石墨晶体的层状结构中C—C键键长为1.43×10^－10m，试求石墨晶体中的层间距。(已知六棱柱体积公式为：1/2×6sin₆₀°×a²×b)

[解] 从石墨晶体中选取一个六棱柱(如图)，六棱柱中每个碳原子被6个六棱柱共用，所以，一个六棱柱所拥有的碳原子数为12×1/6=2。

石墨中六棱柱的体积为V=1/2×6sin₆₀°×(1.43×10^－10)²×b

石墨中每个六棱柱所拥有的碳的质量为2×12g·mol^-1/6.02×10²³mol…1

由石墨的密度可得：

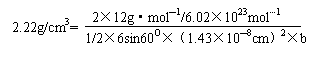
故 b=3.38×10^－8cm=3.38×10^-10 m。

即石墨晶体中的层间距为3.38×10^－10 m

石墨是片层结构，通常的习题中是确定在同一层内，每个六边形所拥有的碳原子数，只考虑同一层时，每个六边形所拥有的碳原子数为2(每个碳与另外三个碳相连，实际拥有1/3，6×1/3=2)，往往容易认为一个六棱柱所拥有的碳原子数为4，这样计算出错。

晶体的计算的难点主要是晶体数学模型的构建和宏观体积、质量、密度与微观粒子的数目、占有的体积、质量等的关系及确定晶胞所拥有的原子数。只要掌握这些特点，思维的深刻性、敏捷性就会不断提高。