化学自习室移动版

在用价层电子对互斥理论来讨论分子的空间构型时，要先确定某中心原子的价层电子数，进而得到价层电子对数。在不同的教材中，确定中心原子价层电子对数目的方法往往有显著区别，但判别结果都能相同。了解这诸多的方法间共同的合理内核，对推广价层电子对互斥理论的应用肯定是会有较大帮助的。

一、计算价层电子数的几种方法^[1]

在计算价层电子数时，可以有多个物理模型供选用。在常见的化学教材或教学参考资料中，可以看到有3种其间有显著不同的计算价层电子对数目的模型，产生3类不同的方法。

(一)元素种类法

元素种类法的特点在于，对非过渡系ABm型分子来说，用配原子的种类来确定它向中心原子提供的价层电子数。它规定：

当H及卤原子作配原子时，每个配原子向中心原子提供1个价层电子；

而当O、S原子作配原子时，它们都并不向中心原子提供价层电子；

而当n(原子作配原子时)，它不仅不向中心原子提供价层电子，反而要从中心原子拉走1个价层电子。

如对SO₂分子。中心S原子有6个价电子，而作为配原子的O原子并不向中心原子提供电子，S的价层电子数仍为6，价层电子数对为3。所以，S原子的电子云呈三角形分布。S原子位于三角形的中心附近，电子云分别指向三角形的三个顶点。考虑到3个电子云，只有2个与O原子结合，另1个被孤电子对占据，分子应该为角型。

(二)电子式法

电子式法则是用分子的点电子式中，电子对及电子组的数目，来确定中心原子的价层电子对数。

它规定：中心原子周围的电子对(包括成键电子对和孤电子对)及电子组数(双键的4个电子、或叁键的6个电子，都只能算是1个电子组)之和，就是中心原子的价层电子对数。

如对SO₂分子。根据八隅体原则写出电子式(如左下图)后，可以看出S原子上方有1孤电子对、与右侧O原子结合用了1电子对、与左侧O原子结合用的是4个电子(双键)——为1个电子组。

这样，属于中心原子的电子对数为1、孤电子对数为1、电子组数为1，合计为3。因而价层电子对数为3。与元素种类法的判断结果相同。

电子式法与元素种类法的另一个区别是，在电子式法中没有可以成单的价层电子数的概念。最小的单位也是1个价层电子对。

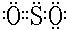
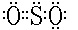
(三)结构式法

结构式法与另两个方法的区别在于，对非过渡系元素构成的分子来说，用结构式中共价键的性质不同，来确定相关配原子向中心原子提供的价层电子数。它规定：

以单键与中心原子结合的配原子，向中心原子提供1个价层电子；

以双键与中心原子结合的配原子，不向中心原子提供价层电子；

以叁键与中心原子结合的配原子，不但不向中心原子提供价层电子，反而要从中心原子拉走1个价层电子。

如对COCl₂分子。根据氧化数或化合价写出结构式(如右上图)后，可以看出：O原子以双键与C原子结合，所以它不向中心原子提供价层电子；Cl原子以单键与C原子结合，每个Cl要向中心原子提供1个价层电子。C的价层电子数就是自己原有的价电子数4，加上2个Cl提供的2个电子，总数为6。其价层电子对数为3。也与元素种类法的判断结果相同。

结构式法及电子式法的优点在于，可以比较容易地把价层电子对互斥理论的适用范围，扩大到有多个中心原子的分子。

如根据化合价把HSCN的结构式写为H－S－C≡N。

将S原子看作中心原子时，S原子原有的价电子数为6、以单键与其结合的H原子向其提供1个电子、以单键与其结合的C原子也向其提供1个电子，这样S原子的价层电子数为8，原子为杂化sp³。H－S－C的键角约为109.5°。

把C原子作为中心原子时，C原子原有的价电子数为4、以单键与其结合的S原子向其提供1个电子、以叁键与其结合的N配原子反而从它那里拉走1个电子，这样中心原子C的价层电子数还是4，为sp杂化。所以S－C－N的键角为180°、三个原子构成一条直线。而H原子不在S－C－N所构成的直线上。

二、元素种类法与总配位数式的统一^[1]

总配位数式是分子组成与结构间固有规律的体现，可以方便地用于由分子的组成来判断其结构。而价层电子对互斥理论，也是用于从分子组成来判断结构的。所以两者间一定会有某种联系。可以证明，价层电子对互斥理论只不过是总配位数式的另一种表现形式而已。

由总配位数式导出价层电子对互斥理论的元素种类法，是十分容易的：

对非过渡元素原子组成的ABm型分子来说，总配位数式可以写为

(I－ 6m) / 2 =Σ……(1)

其中I为分子的价电子总数(分子中所有原子的价电子数之和)，m为分子中的配重原子(配原子、且是重原子)数，Σ为总配位数，即杂化轨道数。

当Σ=2时，中心原子为sp杂化，其两个sp杂化轨道为直线型分布；

当Σ=3时，中心原子为sp²杂化，三个sp²杂化轨道分别指向平面三角形的3个顶点；

当Σ=4时，中心原子为sp³杂化，四个sp³杂化轨道分别指向四面体的4个顶点；

当Σ=5时，中心原子为sp³D杂化，五个sp³d杂化轨道分别指向三角双锥的5个顶点；

当Σ=6时，中心原子为sp³d²杂化，六个sp³d²杂化轨道分别指向八面体的6个顶点.

这就是总配位数反映出来的分子结构信息。

知道了某分子的配重原子数，及其价电子总数，对ABm型分子来说，为简化计算(式(1)中还有Bm项)，可以令中心原子A的价电子数为a，配重原子B的价电子数为b，则I=A＋Bm。将其代入式(1)后就有总配位数式的另一表现形式：

……(2)

如果将总配位数Σ，改称为价层电子对数。这样2Σ就成了价层电子数。

a＋(b－ 6)m= 2Σ……(3)

式(3)可以被解读为：在计算中心原子的价层电子数时，中心原子的价电子数(a)要如数计入；而每个配原子(价电子数为b)所贡献的价层电子数仅是(b－ 6)。

这就是所谓的元素种类法的“实质”，是在元素种类法中“氧配原子不提供电子”的“原因”。

由此看来，价层电子对互斥理论实际只是总配位数式的另一种表现形式而已。

三、电子式法与总配位数式的统一

由上面的分析不难看出，所谓的用元素种类来确定其提供的价层电子数，实际是采用了另一种方法来计算总配位数，来确定中心原子的杂化类型。价层电子对互斥理论是无法绕开中心原子杂化类型——这个核心问题的。

清楚这一点，就不难找到电子式法的“真谛”了。

大家都知道，从杂化轨道的使用情况来看，杂化轨道只能用于与配原子成σ键，或被孤电子对占据。

多数人不会想到，如果有办法先确定出某中心原子所属的σ键及孤电子对的总数，实际上也就是确定出了中心原子的杂化类型。而电子式法恰恰就是这么做的。

下面就分析一下“用电子式中，电子对及电子组的数目来确定中心原子的价层电子对数”这句话的后半段中“电子对”及“电子组”的含义：

在电子式中的电子对，实际上有两种不同的存在形式。一种是位于两个原子之间的、起键连作用的共用电子对，也叫共价单键。这种共价单键无例外地都是σ键。另一种则是表示某杂化轨道已被两个电子占据的孤电子对。对某中心原子来说，属于它的共价单键的数目可能不止1个，孤电子对的数目也可能有多个。所以计算“电子对”数目，实际上就是在计算以单键形式存在的σ键数、及孤电子对数之和。

在电子式中的电子组，实际上也有两种不同的存在形式。一种是与共价双键匹配的由4个电子构成的电子组。另一种则是与共价叁键匹配的由6个电子构成的电子组。而无论在双键、还是在叁键中，都只有1个σ键。所以，计算电子组的数目，实际上实在计算，在多重键中存在的σ键的数目。

这样，计算“电子对及电子组的数目”，就是在计算所有的σ键数、及孤电子对数之和。这就是在计算杂化轨道的总数，就是在计算总配位数。是在在直击“总配位数式”的核心。

总配位数式使用的是数学的方法，而电子式法则是借助于电子式来计算杂化轨道的数目。电子式法从一个侧面证明，总配位数式才是价层电子对互斥理论的核心。

四、结构式法与总配位数式的统一

结构式法无疑也是在计算所讨论原子的总配位数。由于结构式法在计算中心原子的价层电子数时，考虑了中心原子原有价电子数，可以预计结构式法与元素种类法的关联会更密切一些。

与元素种类法比较：

其规则“当H及卤原子作配原子时，每个配原子向中心原子提供1个价层电子”。从结构式的角度来描述，就是“当配原子以单键与中心原子结合时，配原子要向中心原子提供1个价层电子”。因为，“当H及卤原子作配原子时”，配原子都只能以单键的形式与中心原子相连。

其规则“当O、S原子作配原子时，它们都并不向中心原子提供价层电子”。从结构式的角度来描述，就是“当配原子以双键与中心原子结合时，配原子并不向中心原子提供价层电子”。因为，“当O、S原子作配原子时”，配原子都只能以双键的形式与中心原子结合。

其规则“当N原子作配原子时，它不仅不向中心原子提供价层电子，反而要从中心原子拉走1个价层电子”。从结构式的角度来描述，就是“当配原子以叁键与中心原子结合时，配原子不仅不向中心原子提供价层电子，反而要从中心原子拉走1个价层电子”。因为，“当N原子作配原子时”，配原子都只能以叁键的形式与中心原子成键。

可见，结构式法是在借用元素种类法的成键情况来计算总配位数。这也意味着，结构式法是由元素种类法演变而来的，与总配位数式也是一致的。

虽然结构式与电子式有相通之处，但在计算价层电子数时，两者间并无直接的演变关系。这也使我们想到，在用结构式法来判断某原子的杂化类型时，要特别注意结构式的来源。因为结构式可能从两个不同的途径而得到。一个是由电子式改写出来，另一个则是用化合价匹配来获得。两者的形式有可能不同。

如对SO₂分子，由电子式得到结构式(如下左图)。其中，有1个S=O双键、1个是S原子单方面提供电子对给O原子的σ配键。这会给价层电子数的计算带来一定的麻烦。

由其中心S原子化合价为＋4，也可以得到一个结构式(如下右图)，其中有2个双键(由化合价写出的结构式中不会有配键)。用这一结构式来计算价层电子数则很方便。

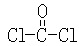
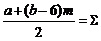
在使用结构式法来确定价层电子数时，要注意到这一结构式来源不同的区别。

参考文献

[1]伍伟夫总配位数式与价层电子对互斥理论.化学原理补正博客