化学自习室移动版

1998年高中学生化学竞赛（初赛）第5题涉及晶胞概念。1999年全国高考化学试题第33题本不必借助晶胞概念就能得解，但许多人却将之与去年竞赛题联系起来，认为引入晶胞概念会有助于解题，引发了如图1氯化钠晶胞究竟是实线小立方体呢还是虚线大立方体的争论。还有人问: 为什么说氯化钠是面心立方晶胞? 有没有一种简单的方法判断某晶体是简单晶胞抑或面心晶胞、体心晶胞？这使笔者联想起1998年4月28日某发行量极大的面向中学生的刊物的第一版上有一篇题为《对晶体空间结构的分析》的文章错误地称：“NaCl晶体是一种简单立方......。”“CsCl晶体是一种立方体心......。”“干冰晶体是一种立方面心......。”等等。本文由此而发。

晶胞概念是晶体学基本概念，本应在建立点阵概念后再作讨论，但点阵概念较抽象，许多读者或称虽学过却天长日久忘了，或称原先就稀里糊涂，眼下也无精力时间再去深抠，要求笔者撇开点阵概念讨论晶胞。笔者被逼无奈，作了几次尝试，渐渐形成一篇讲稿，听讲人觉得接受起来轻松得多，现特将这份被逼出来的讲稿整理加工如下，以谢诸公相助。

一、晶胞具有平移性

晶胞是描述晶体微观结构的基本单位。分析一个晶胞中原子的排列，就等于分析了整块晶体。整块晶体可视作成千上万个晶胞“无隙并置”地堆积而成。所谓“无隙”，指晶胞与晶胞总是共面共顶角共棱地比邻，晶胞间不留任何空隙；所谓“并置”，是指从一个晶胞到另一个晶胞，无须转动，是简单平移，或者说，晶体是由许许多多方向完全一致的晶胞在晶体微观空间的任何一个方向上平行地排列着的，晶体中不存在取向不同的晶胞。其实，“无隙并置”是晶胞本质特征—“平移性”的另一表述而已。

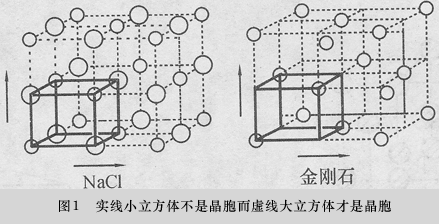
     晶胞具有平移性，因而，观察一个晶胞，绝对不能把它当作游离孤立的几何体，而需“想见”它的上下左右前后都有共面共顶共棱的完全等同的晶胞与之比邻。晶胞的平移性决定了：晶胞的顶角、平行面、平行棱一定是等同的。由此就不难判断，例如图1中的实线小立方体不是“氯化钠晶胞”和“金刚石晶胞”，十分明显，它们的顶角不等同，反之，其8倍体积的虚线大立方体才分别是氯化钠和金刚石的晶胞，其上下左右前后都有等同比邻晶胞，虽未在图中画出，却不应不想见，这点想象力大家都有，只是有时忘记了，才引出错误。

诚然，实际晶体跟被看作简单平移无隙并置的晶胞堆积而成的理想模型是有差别的，实际晶体经常出现各种缺陷，例如，按理想模型该有原子的地方可能缺失了原子或被另一种原子替代了，而不该有原子的地方可能嵌入了某个原子，晶胞与晶胞也可能发生位错，并非完全“并置”，甚至近年还发现许多晶体中原子重复出现的周期并不单调而有涨落而被称为“非公度晶体”。实际晶体的许多独特性质正与这些偏离理想模型的结果。但这些事实不能动摇晶体理想模型的基础地位，因为晶体缺陷的浓度一般仅万分之几而已。

二、晶胞是平行六面体

图2中的5种多面体均可具平移性, 可无隙并置, 可用作晶胞，称为费多罗夫体，19世纪中叶俄国晶体学家费多罗夫（E. S. Fedorov）正是通过考察这5种多面体的拓扑变形（图2最右两图是正六方柱体变形的个别例子）呈现的对称性，推证出晶体三维微观对称类型—230空间群，竖起人类思想史上的一块丰碑（见E. S. Fedorov，Symmestry of Crystals，ACA Monograph，1971）。还有所谓布里渊体（Brilliouin zone，例如图3的多面体），也叫魏格纳-塞茨晶胞（Wigner-Seitz cell）或第里希勒体（Dirichlet region），其中有的与费多罗夫体相同，有的则为更复杂的多面体，却也具有平移性，可无隙并置, 也符合晶胞的定义（见B. K. Vainshtein，V. M. Fridkin，V. L. Indenbom，Modern Crystallography II，Springer，1982）。这些非习用晶胞对某些晶体学研究很有意义，如晶体中的电子运动的量子力学方程的建立，但现今大家习用的三维晶胞却只是一种费多罗夫体—平行六面体，最早由法国科学家布拉维（Bravais）提出，全名当为“布拉维晶胞”。约定俗成，通常谈论的晶胞，是“习用晶胞”，总是指布拉维晶胞，是平行六面体。

5种费多罗夫体（上左1-5）；

正六方柱体变形举例（上右两图）；

费多罗夫体无隙并置举例（下三图）

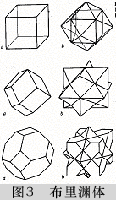
图 2 各式各样可作晶胞的多面体图3 布里渊体 

于是，如图2的六方柱体就并非现今意义的布拉维晶胞。因而，某教学参考资料认为金属锌的晶胞是六方柱体是不符合约定俗成的习用晶胞（布拉维晶胞）定义的，尽管如前所述，六方柱体不能说不可当作晶胞来考察，但不是当今的习用晶胞，易造成初学者概念混乱，在基础课程中以不采纳为宜。

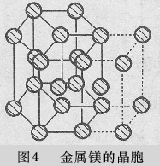
还见到某教学参考资料说，如图4的六方柱体由三个布拉维晶胞构成，其底面中心的原子为6个布拉维晶胞共用。这个错误是严重的，因为，构成六方柱的三个平行六面体虽无隙却非并置，从一个平行六面体到另一个平行六面体不仅移动而且旋转，不符合晶胞具有平移性的本质属性，因而我们只能取其一为晶胞而不能同时取其三。设取其前右平行六面体为晶胞，则其相邻晶胞为如虚线所画的平行六面体，上下左右前后全都是如是方向的平行六面体，决非另两个实线围拢的平行六面体。于是，晶胞所有顶角就没有任何差别，顶角的原子永远为8个晶胞共用，决不可能有6个晶胞共用的顶角。需特别注意的是，通常画六方晶胞总是画出一个立方柱体是为更鲜明地描绘出晶体中的原子的对称分布，并非表明六方柱体是六方晶胞。

 三、布拉维系的七种晶胞

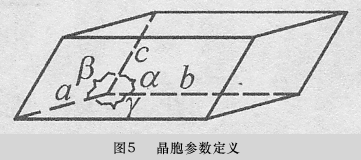
按平行六面体的几何特征（晶胞的边长a、b、c和夹角α、β、γ，注意：夹角定义参见图5，有一通用教科书画错）可将晶胞分为立方cubic（a=b=c，α=β=γ=90o，只有一个晶胞参数a）、四方tetragonal（a=b≠c，α=β=γ=90o，有2个晶胞参数a和b）、六方hexagonal（a=b≠c，α=β=90o，γ=120o，有2个晶胞参数a和c）、正交orthorhombic（a≠b≠c，α=γ=90o，有3个晶胞参数a、b和c）、单斜monoclinic（a≠b≠c，α=γ= 90o，β≠90o，有4个晶胞参数a、b、c和β）、三斜triclinic（a≠b≠c，α≠β≠γ，有6个晶胞参数a、b、c、α、β和γ）和菱方rhombohedral（a = b = c，α=β=γ≠90o，有2个晶胞参数a和α）七种，见图6。

图6 布拉维系的七种晶胞

在1983年出版的晶体学权威著作（Hahn, T. International Table for Crystallography, Vol. A, REIDEL Publ. Comp. 1983）中把用上述七种晶胞描述晶体结构的体系正名为布拉维系（Bravais system），我国教科书至今未这样做。

需要附带指出的是，布拉维系与七大晶系（crystal system）并不一一对应，其交错之处为：七晶系中无菱方而有三方；三方晶系有的属菱方布拉维系（取菱方晶胞），有的却属立方布拉维系（取六方晶胞）。此外，还有一种六晶系的体系，其六方晶系是七晶系的六方和三方的合并，上引1983年国际晶体学表已将其正名为crystal family，笔者曾建议译为“晶族”，以与晶系向区别。关于这个问题有待另撰它文讨论，本文讨论晶胞避开了对称性概念，而晶系概念舍弃对称性是很难谈清楚的，只得从略不谈了。但仍需指出，至今，世界各国，普遍存在七晶系、六晶族和七晶胞的布拉维系各唱各的调，都叫“晶系”的现象，还有许多不恰当的、混杂的“晶系”，三言两语还真难说清。笔者认为，中学、大专、本科低年级基础课不宜讨论晶系，以采用布拉维系为好，布拉维系有晶胞图形，无须对称性知识基础，对初学者是容易接受的。对晶系概念感兴趣的读者可以阅读拙著《混乱的晶系》，大学化学杂志第2000年第1期。

四、晶胞中原子的坐标与计数

晶胞中的原子可用向量xa + yb + zc中的x, y, z组成的三数组来表达它在晶胞中的位置，称为原子坐标，如，位于晶胞原点（顶角）的原子的坐标为0，0，0；位于晶胞体心的原子的坐标为1/2，1/2，1/2；位于ab面心的原子坐标为1/2，1/2，0；位于ac面心的原子坐标为1/2，0，1/2；等等（图7）。坐标三数组中数的绝对值^②的取值区间为1＞|x（y，z）|≥0。若取值为1，相当于平移到另一个晶胞，与取值为0毫无差别，可形象地说成“1即是0”。因而，位于晶胞顶角的8个原子的坐标都是0，0，0，没有差别，它们中的每一个原子均为相邻的8个晶胞共用，平均每个晶胞只占1/8。而且，只要一个顶角上有原子，其他7个顶角上也一定有相同的原子，否则就失去了平移性，不是晶胞。同样道理，坐标为1/2，1/2，0的原子是指两个平行的ab面的面心原子，而且有其一必有其二，否则也失去平移性，晶胞不复存在。反之，坐标不同的原子即使是同种原子，在几何上也不同，不能视为等同原子^③，例如，坐标为1/2，1/2，0的原子与坐标为0，1/2，1/2的原子是不同的。由此可见，当原子处于晶胞顶角，每个晶胞平均有8×1/8=1个原子；当原子处在面上，每个晶胞平均有2×1/2 = 1个原子；当原子处于棱上，每个晶胞平均有4×1/4= 1个原子；等等。毋容置疑，如果原子处在晶胞内，则有一个算一个。
　　　　
　　 [讨论题]给出金刚石晶胞中各原子的坐标。答案略。

五、素晶胞与复晶胞(体心晶胞、面心晶胞和底心晶胞)

有一个真实的故事：有一次我的一个学生写了一份讲晶胞的讲稿，把晶胞说成晶体的“最小平移单位”，我读后把“最小”改为“基本”，指出晶胞不一定是晶体微观空间的“最小”平移单位，写稿人却并不体会，仍不能改掉晶胞是“最小”平移单位的说法。这一错误是忘记了有两类晶胞——素晶胞和复晶胞。只有素晶胞才是最小平移单位，是不可能再小的晶胞，而且，它的内容物，即晶胞内的原子的集合是微观晶体周期性平移的最小单元，即结构基元；然而，人们有时并不用素晶胞来表达晶体结构，例如，氯化钠晶体，其素晶胞是一个夹角60^o的菱方晶胞，可是通常人们都用比这个素晶胞大得多的面心立方晶胞来表达氯化钠结构，后者是复晶胞，其内容物是素晶胞的4倍。为什么这样呢？原来，晶胞的取用，首先必须反映晶体的微观对称性（230空间群），然后人们才选取尽可能小的体积^④。这两个条件是分先后满足的，于是，如果选用素晶胞不能充分反映晶体的微观对称性，就不得不选用复晶胞。为满足部分读者,我将在本文最后专门讨论这个问题。总之，复晶胞是素晶胞的多倍体，分体心晶胞（2倍体），符号I，面心晶胞（4倍体），符号F，和底心晶胞，符号A、B或C（2倍体）三种。
　　体心晶胞的特征是可作体心平移；反之，不能作体心平移的晶胞不是体心晶胞。检验晶胞内的原子是否存在体心平移关系最简单的方法是：将晶胞的框架（围拢晶胞的多面体）的顶角移到原晶胞的体心位置（晶胞内外原子的位置保持在原位不动），考察一下：移位的框架围拢的“新晶胞”里所有原子的位置是否与原晶胞里所有原子的位置一一对应地相等，如果相等，表明晶胞具有“体心平移”的特征，这种晶胞就是体心晶胞，若不是，这种晶胞就不是体心晶胞。在晶体学上，体心平移用+（1/2，1/2，1/2）来表示，意思是原晶胞中的半数原子与另半数原子的关系是在它们的坐标加上1/2，1/2，1/2 的向量发生“分数平移”的关系。例如，体心球是顶角球的坐标0，0，0加1/2，1/2，1/2，即发生体心分数平移的产物。上面我们移动晶胞的“框架”得到的“新晶胞”中的任一原子与原晶胞位置相同原子的关系正是这种分数平移关系。因此，

体心晶胞中原子的数目等于“结构基元”的2倍。
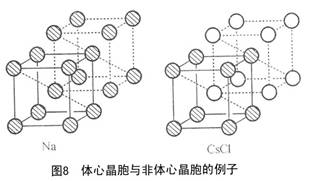
　　[讨论题] 图8中哪个晶体的晶胞（用实线围起）是体心晶胞？
　　[答案]金属钠的晶胞是体心晶胞，可作体心平移，所得用虚线围起的新晶胞与原晶胞中所有原子的坐标相同；氯化铯的晶胞不是体心晶胞，不能作体心平移，原晶胞的“框架”移动后，所得“新晶胞”（虚线围起）里的氯原子和铯原子的原子坐标与“原晶胞”不同。
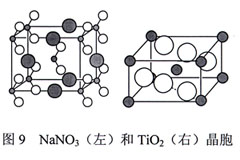
　　[讨论题]图9的亚硝酸钠和金红石（TiO₂）晶胞哪个是体心晶胞？为什么？
　　[答案] 亚硝酸钠是体心晶胞，金红石是素晶胞。
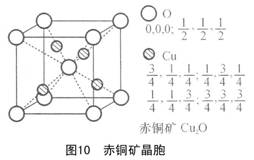
　　[讨论题]赤铜矿晶胞（a = 426 pm）（图10）是否体心立方晶胞？
　　[答案]不是体心立方晶胞。若将体心氧原子改为晶胞原点，原晶胞的“框架”平移后得到的新晶胞中铜原子的坐标是1/4，1/4，1/4，……，与原晶胞不同，因此不能作体心平移。该晶胞是素立方晶胞。
　　　
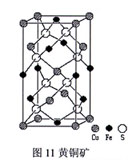
　　[讨论题] 黄铜矿晶胞是体心四方晶胞吗（图11）？

[答案] 是体心四方晶胞。

面心晶胞的特征是可作面心平移，将原晶胞框架的顶角平移原晶胞的任一面心位置得到的新晶胞与原晶胞无差别。说明原晶胞里的原子可以分成4等份，其中3份原子是第一份原子作面心平移的产物。因此，面心晶胞中的原子是结构基元的4倍。在晶体学上，面心平移的符号是+（1/2，1/2，0；0，1/2，1/2；1/2，0，1/2）。
　　[讨论题]图12中哪些晶体的晶胞是面心晶胞？

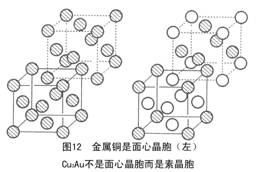
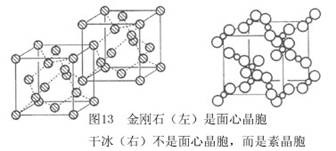
[讨论题]金刚石、钙钛矿、干冰的晶胞是不是面心晶胞（图13）？

底心晶胞的特征是：将晶胞的框架的顶角移至晶胞的某一对面的中心所得的新晶胞与原晶胞无差别。说明晶胞里的半数原子是另半数原子作“底心平移”的产物，即该晶胞是结构基元的2倍体。在晶体学上底心平移的符号是+（1/2，1/2，0）（C底心）；或+（0，1/2，1/2）（A底心）；或+（1/2，0，1/2）（B底心）。底心平移是指其中之一。底心晶胞较少，图14的碘是底心晶胞的一个例子。
　　
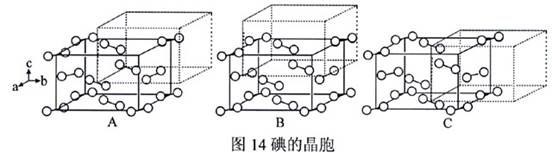
　　图14的A、B、C编序与底心符号是一致的（参考图中的坐标系），但只有将晶胞框架的顶角移至ac面的面心，所得新晶胞才与原晶胞无差别，若移至bc面心或ab面心，得到的新晶胞中的原子坐标不同于原晶胞，因此不能作A或C平移，故碘是B底心（注意：底心符号是与坐标系匹配的，若颠倒长短轴的顺序，底心符号自然会改变，因而可能别的书上碘的底心符号与本文不同）。
　　注释：
　　① 单斜晶胞的取向常见有两种，一种定义β≠90o, 另一种定义γ≠90o，前者为化学家习用。“菱方”是本文作者的建议译名，其原文是“rhombohedral”，《化学化工词典》译为“菱面体”。有些国内外教科书和科学文献中把它称为“trigonal”，译为中文是“三方”，这些教材和文献的提法与晶体学权威著作《晶体学国际表》（1983）是不一致的，应予以纠正才是。
　　② 有时为说明晶胞中原子的对称关系，原子坐标常取负数，如“3/4”也可写成“－1/4”等。
　　③ 这里“等同”的英文是identical。等同原子（identical atoms）是指通过x，y，z为整数值的平移能够重复的原子。在晶体学里还常使用equivalent一词来讨论晶胞中原子的相关性，后者不应译为等同，而应译为等效或等价。等效原子（equivalent atoms）是指通过镜面反映、旋转轴旋转等等对称操作相互变换的原子。
　　④ 有的书还增加一个选取晶胞的原则：“尽可能多的直角”。其实，晶胞有多少直角，是晶体对称性决定的，不是愿意多少的问题。