化学自习室移动版

晶体结构是近几年来高考考查的重点和热点，特别是晶体结构的计算更是其中的重中之重，它体现了高考考试说明中提出的“将化学问题抽象为数学问题，利用数学工具，通过计算推理解决化学问题的能力”的要求。化学教学中，让学生学习和探究原子、离子、晶体结构等微观结构内容，可以促进学生形成比较丰满的三维空间概念，有效地带动学生进行丰富多样的三维空间想像。通过氯化钠、氯化铯、金刚石、石墨、干冰、二氧化硅等曲型晶体结构模型为落点来设计问题考查学生的三维空间思维能力。

一、离子晶体：

例1、图中NaCl晶体结构向三维空间延伸得到完美晶体。最近的Na⁺与Cl^-核间距离为a×10^-8cm，求晶体密度?

解析：截取一个1/8大的小立方体如图，因各顶点上的Na⁺或Cl^-为8个小立方体共用，故小立方体占1/2个Na⁺，1/2个Cl^-，即占1/2Na⁺—Cl^-离子对。

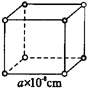
　　立方体体积为：V=（a×10^-8）³cm³

　　故密度：ρ=（（1/2）个×58.5g·mol^-1÷6.02×10²³个·mol^-1）/（a³×10^-24cm³）=（48.6/a³）g·cm^-3

例1：在氯化钠晶体中，与氯离子距离最近的钠离子有    个；与氯离子距离最近的氯离子有         个。 

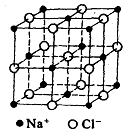
     解析：我们可以选定中心的氯离子作为基准，设立方体的边长为a，则氯离子与钠离子之间的最近距离为，此钠离子位于立方体六个面的面心上，即有六个钠离子；氯离子间的最近距离为，共有12个。

例3．有下列离子晶体结构示意图：●阳离子○阴离子

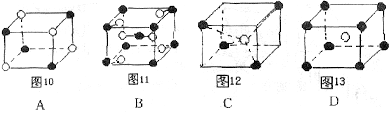
以M代表阳离子、N代表阴离子。

（1）请写出各离子晶体组成的表达式：

A_______，B________，C____________，D_________。

（2）已知黄铁矿的主要成份FeS₂晶体具有A的空间结构。晶体中具有化学键类型是______________，若晶体结构Ａ中相邻的阴阳离子间距离为acm，N₂代表阿伏加德罗常数，则FeS₂晶体的密度是___________g/cm²。

分析：（1）分析图10，离子都在立方体的顶点上，每个顶点都被8个类似的立方体共用，所以图10所表示的立方体中共有阳离子个、阴离子个，A的化学式为MN。观察图11，每个立方体单元中有阳离子“”个，阴离子共有“”个，所以B的化学式为。观察图12，每个立方体单元中，共有阳离子“”个，阴离子1个，所以C的化学式为。观察图13，每个立方体单元中共有阳离子“”，阴离子1个，所以，D的化学式为MN。

（2）FeS₂中包含有“非极性共价键（S—S）、离子键”。晶体的密度为。

二、原子晶体及石墨晶体

例5、金刚石结构中，一个碳原子与    个碳原子成键，则每个碳原子实际形成的化学键为    根；a mol金刚石中，碳碳键数为      mol。

解析:从金刚石结构可以看出，一个碳原子与 4个碳原子成键，但一根碳碳键是由两个碳原子形成，即每根碳碳键中，一个碳的原子的贡献为，故金刚石中，一个碳原子的实际成键数=× 4=2。故a mol金刚石中，碳碳键数为 2a mol。

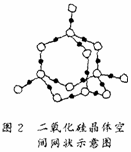
    例6、二氧化硅晶体的结构计算：书本上介绍了二氧化硅晶体平面示意图（图8），图9表示空间网状示意图，图10表示二氧化硅的晶胞。试回答：

（1）30g二氧化硅中含有       molSi-O键。

（2）最小的环上共有     个原子，其中     个氧原子，     硅原子。

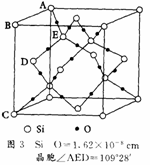
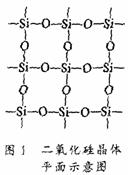
        解析：（1）从图8，可以清楚地看到一个硅原子与周围的四个氧原子成键，故30g二氧化硅中含有的Si-O键为。

（2）从图8看到最小的环上有8个原子（4个硅原子与4个氧子），但图8仅是平面示意图，它只表示了二氧化硅晶体中硅、氧原子的成键情况，而不能表示其立体结构。此时应观察图9，该结构可理解为：金刚石结构中的碳原子换成硅原子然后在两个硅原子之间嵌入一个氧原子。可看到形成的最小环上共有12个原子，其中6个为氧原子，6个为硅原子；Si-O键的夹角为为109°28′。

       例6：分析 石墨结构中 碳原子数与碳碳键数目比。

 解析：我们可以先选取一个正六边形（如图4），此结构中的碳原子数为6 ，而一个碳原子被三个六元碳环共用， 故此正六边形中的碳原子数为6×=2。六边形中的任一条边（即碳碳键）均被2个正六边形共用，故正六边形中的碳碳键数为6×=3，所以碳原子数与碳碳键数目比为2:3。

       我们也可以选取一层原子（设有n个），若不计重复则可形成3n根碳碳键，实际形成的碳碳键数为n根，同样可以计算出碳原子数与碳碳键数目比为2:3。

        例7：C₆₀分子是形如球状的多面体，如图6，该结构的建立是基于如下考虑：①C₆₀分子中每个碳原子只跟相邻的3个碳原子形成化学键②C₆₀分子只含有五边形和六边形。C₇₀分子也可制得，它的分子模型可以与C₆₀同样考虑而推知。通过计算确定C₇₀分子中五边形和六边形数。

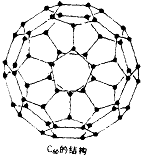
解析：设五边形和六边形数分别为x和y，若形成独立的五边形和六边形所需碳 原子数为5x+6y，由于每个碳原子与相邻的3个碳原子成键，故C₇₀分子中的碳原子数可用    表示。故有如下关系：

=70          ①

再根据欧拉公式，多面体的顶点数、面数、棱边数之间的关系：

顶点数+面数-棱边数=2。对C₇₀分子而言顶点即为碳原子数，面数为五边形和六边形数之和，棱边数为碳碳键数，碳碳键数目共有，故可得出如下式子： 70+（x+y）-×3×70=2      ②

①②联立方程组可解得：x=12   y=25

三、分子晶体

    例2：二氧化碳晶体中，与二氧化碳分子距离最近的二氧化碳分子有       个。

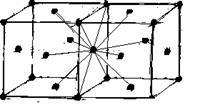
解析：在图2 的二氧化碳分子晶体结构中，8个二氧化碳分子处于正方体的8个顶点上，还有6个处于正方体的六个面的面心上。此时可选定面心的二氧化碳分子为基准，设正方体的边长为a，则二氧化碳分子间的最近距离为，从图中看有8个，它们分别位于该侧面的四个顶点及与之相连的四个面的面心上。此时应注意，图中所给出的结构仅是晶胞。所谓晶胞，是晶体中最小的重复结构单元，它能全面正确地表示晶体中各微粒的空间关系。也就是说晶体是以晶胞为核心向空间延伸而得到的，单个的晶胞不能表示整个晶体的结构。所以在我们观察晶体结构时应充分发挥空间想象的能力，要将晶胞向各个方向（上，下，左，右，前，后）扩展。图2向右扩展 得图3(为容易观察,用表示二氧化碳分子)，从中可以看出与二氧化碳分子距离最近的二氧化碳分子有 12   个。                               

从以上的分析可以看出，要正确确定晶体中距离最近的微粒的数目，首先要对晶体结构熟悉，其次要有良好的空间想象能力，要有以晶胞为核心向空间扩展的意识。

总之，晶体结构的有关计算是将化学知识和数学中的立体几何，物理中的晶体结构问题紧密联系的一种学科间综合题，有较大的难度。通过晶体结构计算习题的训练能够培养学生的空间想象能力和运用数学工具解决化学问题的能力，从而提高学生的综合素质和能力，这是高考向“3+x”综合方向发展的必然趋势。