化学自习室移动版

  “守恒法”是中学化学经常采用的技巧性解题方法之一。

  一般情况下，能用“守恒法”解答的题目也能用其它方法解决，但较费时且易出错。而 “守恒法”则是利用物质变化过程中某一特定量固定不变来解决问题，其特点是不纠缠于细枝末节，只关注始态和终态，寻找变化前后特有的守恒因素，快速建立等式关系，巧妙作答，能提高解题速率和准确率。

 “守恒法”在不同版本的教辅材料中，有多种表述形式，如物料守恒、质量守恒、元素守恒、原子守恒、离子守恒、电荷守恒、电子守恒、物质的量守恒、体积守恒…等等。其实所谓的“守恒”因素不外乎三种情况：一是物料守恒，二是电性电量守恒。 

一、物料守恒

 所谓“物料”，就是物质。从物质的形态而言，有宏观意义上的物质，又有微观意义上的粒子。当谈到“物料”守恒时，对宏观物质而言，主要是质量守恒；对微观粒子而言，则主要是与物质的量挂钩的元素守恒。

(一)质量守恒

在此探讨的质量守恒，已不再是狭义的质量守恒定律，它涵盖了物理和化学两种变化中的有关守恒关系。

1.固态混合物

由固体物质组成的混合物，往往在化学变化前后存在某一方面的守恒因素，利用这些因素可省时省力。

例1：取一定量的KClO₃和MnO₂的混合物共热制取O₂，反应开始时MnO₂在混合物中的质量分数为20%，当反应进行到MnO₂在混合物中的质量分数为25%时，求KClO₃的分解百分率。

解析：MnO₂在反应中作催化剂，反应前后质量守恒。设原混合物的质量为m₁g，反应结束后混合物的质量为m₂g，则MnO₂反应前后的质量分别为：0.2m₁g和0.25m₂g。由MnO₂的质量守恒可得：0.2m₁g＝0.25m₂g，m₂＝0.8m₁。由反应前后质量守恒可知，放出O₂的质量应等于反应前后的固体质量之差，即：m₁g-m₂g＝m₁g-0.8m₁g＝0.2m₁g。

即可求得KClO₃的分解百分率为：。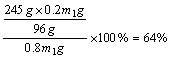

 2.溶液

对溶液而言，可以从其组成上，即浓度（质量分数）、溶剂和溶质三方面去寻找内含的某些守恒因素，用于解决有关溶液计算的问题。

(1)浓度守恒

例2：某盐的饱和溶液的质量分数为26.8%，取一定量的此饱和溶液，加入wg该无水盐，在温度不变的情况下，析出mg含有一定量结晶水的该盐晶体，则从饱和溶液中析出溶质的质量为

A.26.8%w              B.m-w                 C.(m+w)×26.8%       D.(m-w)×26.8%

解析：由于温度不变，析晶后，剩余溶液、减少的溶液（m-w）及原溶液浓度（质量分数）守恒，故有（m-w）×26.8%，答案应选D。

(2)溶剂守恒

 例3： 在一定温度下，向55.3g蒸馏水中加入一定量的无水Na₂SO₃粉末，充分搅拌后过滤，得到60g滤液和一定量的Na₂SO₃·7H₂O晶体，若此温度下Na₂SO₃的溶解度为20g，求析出的Na₂SO₃·7H₂O晶体的质量。

解析：解此题的关键是：溶剂水的质量守恒。析晶后，原溶剂水分成了两部分，即所得饱和溶液中的水和析出晶体中的结晶水。若设析出晶体的质量为xg。则，解得：x=10.6g。

(3)溶质守恒

例4：将某二价金属R的单质粉末投入到200mL浓度为1mol/L的H₂SO₄溶液中，待完全反应后滤去过量的金属粉末，蒸发溶液到剩余84g时，保持温度为t℃，开始析出RSO₄·7H₂O晶体。在该温度下继续蒸发，当析出20.5g晶体时，还留下49g溶液。求金属R的相对原子质量。

解析：由题意可知，84g溶液和49g溶液皆为t℃时的饱和溶液。设RSO₄的摩尔质量为M，RSO₄在t℃时的溶解度为Sg。由溶质的质量守恒可得：

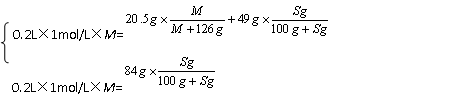
 解方程组得：S=40，M=120g/mol

所以，金属R的相对原子质量为：120-96=24。

3.其它

有些混合体系中，不同形态的物质（如气态和固态或液态，固态和液态等）之间往往会存在某种形式的守恒量，利用这些量之间的守恒关系，可使问题得以简化。

例5：向一定量的NaOH固体中加入由硫酸铜和硫酸组成的混合物的溶液，充分搅拌，恰好完全反应，有蓝色沉淀生成，过滤，所得滤液的质量与加入的原混合物溶液的质量相等。则与硫酸铜反应的氢氧化钠和与硫酸反应的氢氧化钠的物质的量之比为      。

解析：此题属于一道典型的无数据计算题。依题意不难分析出其中的守恒关系，即m(NaOH)＝m[Cu(OH)₂]。设与CuSO₄反应的NaOH为xmol，与H₂SO₄反应的NaOH为ymol，

则由(xmol+ymol)×40g/mol＝98g/mol×(xmol×)，。

 (二)物质的量守恒

在大多数资料中，对物质的量守恒描述的并不多，其实我们最常遇到的元素守恒就隶属于其中。当然还有涉及宏观（具体）物质的守恒。

1.涉及宏观（具体）物质的守恒

例6：质量分数为a的某物质的溶液mg与质量分数为b的该物质的溶液ng混合后，蒸发掉pg水。得到的溶液每毫升质量为qg，物质的量浓度为c。则溶质的分子量（相对分子质量）

A.          B.

C.        D.

解析：根据溶质的物质的量守恒可得：L/mL×cmol/L，整理得：g/mol，故选C。

2.元素守恒

实际上，元素守恒也含有质量守恒的意思，只不过在具体应用时，很少直接用其质量而是用其物质的量（或粒子个数）。元素守恒又可分为原子守恒和离子守恒，但原子守恒和离子守恒并没有严格意义上的区分，只是由于在不同情境中呈现的形态不同而已，多数情况下，常笼统地称作元素守恒。

(1)原子守恒

例7：某温度下，1L密闭容器中加入1molN₂和3molH₂，使反应达到平衡。测得平衡混合物中N₂、H₂、NH₃的物质的量分别为M、N、Q。如果温度不变，只改变初始物质的加入量，而要求M、N、Q维持不变，则N₂、H₂、NH₃的加入量用x、y、z表示时，应满足条件：

(1)若x=0，y=0，则z=      。

(2)若x=0.75mol，则y=      ， z=      。

(3)x、y、z应满足的一般条件是（用含x、y、z的方程式表示）        。

例8：将amolH₂S和1molO₂置于一个容积可变的容器内进行反应。维持容器内气体的压强不变（101kPa），在120℃下测得反应前后容器内气体的密度分别为d₁和d₂。若a的取值不同，则H₂S的氧化产物可能有如下三种情况：

(1)全部是SO₂，此时a的取值范围是       。

(2)全部是S，此时a的取值范围是        ，d₁     d₂（填大于、小于或等于）。

(3)部分是SO₂，部分是S，此时a的取值范围是      ，反应所生成的SO₂的物质的量为   mol，容器内气体的物质的量之和为    mol。（以含a的代数式表示）

解析：n(O₂)=1mol，设生成SO₂为xmol，S为ymol，H₂O为zmol。直写方程式：aH₂S+[1]O₂=xSO₂+yS+ zH₂O(g)。

(1)若y≤0，则全部生成SO₂：

 解得a=，即a的取值范围是：a≤。

(2)若x≤0，则全部生成S：

 解得a=2，即a的取值范围是：a≥2。

(3)若x＞0，y＞0，则产物中既有SO₂，又有S：

由S原子守恒：x+y=a

由H原子守恒：2z=2a

由O原子守恒：2x+z=2

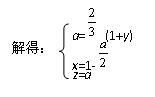
  因为y＞0，从(2)可知y≤2，所以a的取值范围是：＜a＜2。 

反应后，SO₂的物质的量为(1-)mol，容器内气体的物质的量之和为：x+z=(1+)mol。

例9：将2molH₂O和2molCO置于1L容器中，在一定条件下，加热至高温，发生如下可逆反应：

(1)当上述系统达到平衡时，欲求其混合气体的平衡组成，则至少需要知道两种气体的平衡浓度，但这两种气体不能同时是    和     ，或     和    。（填它们的分子式）

(2)若平衡时O₂和CO₂的物质的量分别为n(O₂)_平=amol，n(CO₂)_平=bmol。试求n(H₂O)_平=        。（用含a、b的代数式表示）

（2）由O原子守恒可知，由CO生成CO₂分子内增加的O原子来源于H₂O，另外O₂中的O原子也来源于H₂O。因此，n(H₂O)_反应=2×n(O₂) +1×n(CO₂)=2×amol+1×bmol=(2a+b)mol。n(H₂O)_平=2mol-(2a+b)mol=(2-2a-b)mol。

 (2)离子守恒

例10：向含0.01mol AlCl₃的溶液中逐滴加入34mL 1mol/L NaOH溶液，则生成物及其物质的量分别为                      。

解析：n(NaOH):n(AlCl₃)=0.034mL×1mol/L:0.01mol=3.4:1(或17:5)，大于3小于4，故生成物中既有Al(OH)₃，又有NaAlO₂。设生成的Al(OH)₃的化学计量数为x，NaAlO₂的化学计量数为y。

直写方程式：5AlCl₃+17NaOH=xAl(OH)₃↓+yNaAlO₂+15NaCl+H₂O 

则n[Al(OH)₃]=0.006mol，n(NaAlO₂)=0.004 mol, n(NaCl)= 0.003mol。

 (3)原子、离子并存守恒（元素守恒）

例11：将一定质量的镁、铝合金投入100mL一定浓度的盐酸中，合金全部溶解，向所得溶液中滴加5mol/L的NaOH溶液至过量，生成沉淀的质量与加入NaOH溶液的体积关系如图所示。由图中数据分析计算：

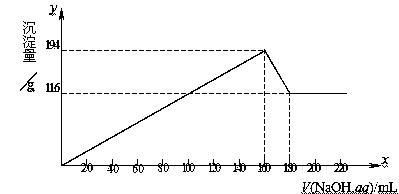
(1)原合金中镁、铝的质量；

(2)盐酸的物质的量浓度。

解析：由图可知：Mg(OH)₂的质量为11.6g，Al(OH)₃的质量为19.4g-11.6g=7.8g。

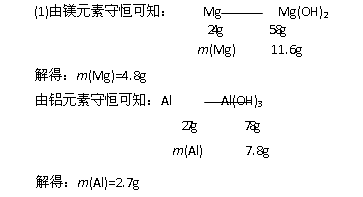
 (2)当V(NaOH,aq) =160mL时，Mg²⁺、Al³⁺完全沉淀，此时溶液为NaCl溶液，由Cl^-离子、Na⁺离子守恒可知：

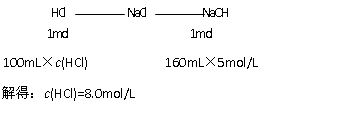
 例12：向300mL KOH溶液中缓慢通入2.24L CO₂气体（标准状况），充分反应后，在减压低温下蒸发溶液，得到11.9g白色固体。请通过计算确定此白色固体的组成及其质量各为多少克？所用KOH溶液的物质的量浓度是多少？

解析：先由极端假设法确定白色固体的组成：设定2.24L CO₂与KOH溶液反应所得产物只有一种，即K₂CO₃或KHCO₃。若只生成K₂CO₃，由C原子守恒可求得m(K₂CO₃)=×138g/mol=13.8g；若只生成KHCO₃，由C原子守恒可求得m(KHCO₃)=×100g/mol=10.0g。而题设质量为11.9g，故该白色固体由K₂CO₃和KHCO₃组成。由C原子守恒可得：n(CO₂)=n(K₂CO₃)+n(KHCO₃)==0.100mol。设K₂CO₃的物质的量为amol，则KHCO₃的物质的量为0.100mol-amol。则由138g/mol×amol+100g/mol×(0.100mol-amol)=11.9g，解之得：a=0.050mol。

所以m(K₂CO₃)=0.050mol×138g/mol=6.90g, m(KHCO₃)=0.050mol×100g/mol=5.00g。

由K⁺离子守恒可得：n(KOH)=2×n(K₂CO₃)+1×n(KHCO₃)= 2×0.050mol+1×0.050mol=0.150mol。

所以c(KOH)=n(KOH)/V=0.150mol/0.300L=0.50mol/L。 

 (4)质子守恒

一般情况下，很少单独考虑质子守恒，实际上在盐（水）溶液中存在的质子守恒可看作是物料守恒与电荷守恒（后面将要涉及到）的叠加项。

所谓的质子守恒，实质是从水的电离出发，考虑弱酸根离子结合水电离出的H⁺或弱碱阳离子结合水电离出的OH^-，然后在溶液中寻找H⁺和OH^-的“藏身”之所，而列出的等式关系。常用于盐溶液中粒子浓度关系的比较。

下面以Na₂CO₃溶液、NH₄Cl溶液和(NH₄)₂CO₃溶液为例，来确定它们的溶液中各自存在的质子守恒关系。

Na₂CO₃溶液：在不考虑CO₃^2-水解时，水电离出的H⁺与OH^-的物质的量是相等的，但当CO₃^2-水解结合部分水电离出的H⁺后，分别生成了HCO₃^-（结合一个H⁺）和H₂CO₃(结合两个H⁺)，而OH^-未被消耗，因此可列出等式关系：c(OH^-)=c(H⁺)+c(HCO₃^-)+2×c(H₂CO₃)，即Na₂CO₃溶液中的质子守恒。

NH₄Cl溶液：同理，NH₄⁺水解结合的是由水电离出的部分OH^-，生成了NH₃·H₂O，而H⁺未被消耗，因此可列出等式关系：c(H⁺)=c(OH^-)+c(NH₃·H₂O)，即为NH₄Cl溶液中的质子守恒。

(NH₄)₂CO₃溶液：NH₄⁺水解结合的是由水电离出的部分OH^-，生成了NH₃·H₂O；CO₃^2-水解结合部分水电离出的H⁺，分别生成了HCO₃^-和H₂CO₃，H⁺、OH^-都有一部分被消耗，分别寻找H⁺、OH^-在溶液中的“藏身”之所，即可列出下列等式关系：c(H⁺)+c(HCO₃^-)+2×c(H₂CO₃)=c(OH^-)+c(NH₃·H₂O)，即为(NH₄)₂CO₃溶液中的质子守恒。

（二）体积守恒

利用体积守恒的题目相比较而言要少一些，实际上它仍隶属于物质的量守恒。化学平衡中会经常遇到反应前后体积守恒的题目，并用于判断和计算，只不过通常情况下不从守恒角度去认识罢了。

例13：在t℃时，向一密闭容器中充入2mol A和3mol B，发生如下化学反应：    ，平衡后测得各物质浓度有如下关系：c^a(A)·c(B)=c(C)·c(D)。然后在温度不变的情况下，扩大容器容积至原来的10倍，结果A的百分含量始终不变，则这时B的转化率为（   ）

A.60%    B.40%    C.20%    D.无法确定

二、电性电量守恒

带电粒子可分为阴、阳离子和电子。在晶体或溶液中，不论有多少种离子，晶体或溶液总是呈电中性，即阴离子所带负电荷总数一定等于阳离子所带正电荷总数（电性相反、电量相等），即所谓的电荷守恒；在氧化还原反应或电解池中，氧化剂（或在阴极上）所得电子总数与还原剂（或在阳极上）所失电子总数相等，即所谓的电子守恒。

1.电荷守恒

多用于计算、判断溶液中粒子浓度之间的关系。在有关溶液的计算题中，若没有特别说明，则可忽略H⁺、OH^-的影响；而在讨论溶液中粒子浓度之间的关系时，却必须考虑在内。

例14：将aL由(NH₄)SO₄和NH₄NO₃组成的混合溶液分成两等份，一份加入bmol烧碱并加热，刚好把NH₃赶出；另一份需消耗含cmol BaCl₂的溶液，沉淀刚好完全。则原溶液中c(NO₃^-)为        。

解析：由题设不难求得aL混合溶液中含2bmol NH₄⁺和2cmol SO₄^2-。依据电荷守恒可得：1×n(NH₄⁺)=2×n(SO₄^2-)+1×n(NO₃^-)，1×2bmol=2×2cmol+1×c(NO₃^-)×aL，c(NO₃^-)=mol/L。

例15：常温下，将甲酸和氢氧化钠溶液混合，所得溶液pH=7，则此溶液中（   ）

A.c(HCOO^-)＞c(Na⁺)

B.c(HCOO^-)＜c(Na⁺)

C.c(HCOO^-)＝c(Na⁺)

D.无法确定c(HCOO^-)与c(Na⁺)的关系

解析：由电荷守恒可知，c(HCOO^-)+c(OH^-)= c(H⁺)+c(Na⁺)，因pH=7，则c(OH^-)= c(H⁺)，故c(HCOO^-)＝c(Na⁺)，选C。 

例16：天然的和绝大部分人工制备的晶体都存在各种缺陷，例如某种NiO晶体中就存在如图所示的缺陷:一个Ni²⁺空缺，另有两个Ni²⁺被两个Ni³⁺所取代。其结果晶体仍呈电中性，但化合物中Ni和O的比值却发生了变化。某氧化镍样品组成为Ni_0.97O。试计算该晶体中Ni³⁺与Ni²⁺的离子数之比。

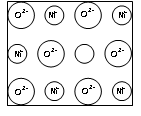
解析：其解法相当多，在此仅讨论守恒法。

法一：设1molNi_0.97O中含Ni³⁺ xmol，则Ni²⁺为(0.97-x)mol。据电荷守恒可得，3×xmol+2×(0.97-x)mol=2×1mol，解得x=0.06mol，则Ni³⁺与Ni²⁺的离子数之比为：0.06mol:(0.97-0.06)mol=6:91。

法二：据电荷守恒直接分析。依题意“一个Ni²⁺空缺，另有两个Ni²⁺被两个Ni³⁺所取代。其结果晶体仍呈电中性，…”从电荷守恒的角度理解：当一个Ni³⁺取代一个Ni²⁺后，正电荷增加1[(+3)-(+2)]，若要保证晶体呈电中性，就必须再增加一个正电荷，也就是说，每当有一个Ni²⁺空缺时，需增加两个Ni³⁺（即取代晶体中的两个Ni²⁺）。1mol Ni_0.97O中空缺0.03mol Ni²⁺，那么Ni³⁺应为2×0.03mol=0.06mol。

法三：结合原子守恒。设1mol Ni_0.97O中含Ni³⁺为xmol，Ni²⁺为ymol。

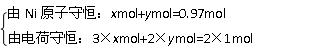
解得：x=0.06mol，y=0.91mol。

2.电子守恒

例17：容积为30mL的试管中充满了NO₂和O₂的混合气体，将试管倒立在水槽中，一段时间后，试管中仍然有5mL气体。则原混合气体中NO₂和O₂的体积比可能是                  。

解析：设原混合气体中有amL NO₂，则O₂为（30-a）mL。

(1)若剩余气体是5mL O₂，那么NO₂完全转化为HNO₃，O₂只有（30-a-5）mL=（25-a）mL被还原。

 由阿伏加德罗定律和电子守恒得：a×1=(25-a)×4，a=20mL，所以V(NO₂) : V(O₂)=20mL : (30-20)mL=2:1。

(2) 若剩余气体是5mL NO，则生成5mL NO消耗的NO₂为15mL，也就是说有(a-15)mL NO₂与(30-a)mLO₂反应生成了HNO₃。

由阿伏加德罗定律和电子守恒得：(a-15)×1=(30-a)×4，a=27mL，所以V(NO₂):V(O₂)=27mL:(30-27)mL=9:1。 

例18：含ng HNO₃的稀硝酸溶液恰好与mg Fe完全反应，若已知有1/4的HNO₃被还原成NO，则n:m的取值范围是            。

三、综合守恒

某些情况下，有的题目可以用不同的守恒关系解决，而有的题目则需要同时运用多种守恒关系方能解决。

1.元素守恒、电荷守恒

例19：向100mL FeCl₃溶液中通入标准状况下的H₂S 2.24L，待H₂S全部被吸收后，再加入过量铁粉，待反应停止后，测得溶液中含有0.6mol金属阳离子，则原FeCl₃溶液的物质的量浓度是        。

解析：有关反应：2FeCl₃+H₂S=2FeCl₂+2HCl+S↓，2FeCl₃+Fe=3FeCl₂，Fe+2HCl=FeCl₂+H₂↑

由此不难发现，通入的H₂S实际上只相当于分解成了H₂和S，对溶液而言并不会产生任何影响，反应前后溶液中恒定不变的是Cl^-离子。 

法一：据Cl^-离子守恒可得：c(Cl^-)×0.100L=0.6mol×2，c(Cl^-)=0.12mol/L,则c(FeCl₃)=×c(Cl^-)=0.4mol/L。

法二：据反应前后正电荷守恒可得：c(Fe³⁺)×0.100L×3=0.6mol×2，c(Fe³⁺)=0.4mol/L，c(FeCl₃)= 0.4mol/L。

 例20：（2003年新课程卷）将0.2mol/L HCN溶液和0.1mol/L NaOH溶液等体积混合后，溶液显碱性，下列关系式中正确的是（）

A.c(HCN)＜c(CN^-)              

B.c(Na⁺)＞c(CN^-)

C.c(HCN)-c(CN^-)= c(OH^-)      

 D.c(HCN)+c(CN^-)=0.1mol/L

2.元素守恒、电子守恒

    例21：用石墨电极电解500mL含KNO₃和Cu(NO₃)两种溶质的溶液，一段时间后，在两个电极上均生成11.2L气体（标准状况下）。试求：

(1)原溶液中c(Cu²⁺)； 

(2)电解后溶液中c(H⁺)(忽略溶液体积的变化)。

解析：根据题中信息可知：

(1)依据电子守恒：(O₂)=(H₂) +0.5L×c(Cu²⁺)×2，

解得，c(Cu²⁺)=1.0mol/L。

(2)依据原子守恒可得:Cu(NO₃)₂~2NO₃^-~2HNO₃~2H⁺则溶液中c(H⁺)=2×c(Cu²⁺)=2.0mol/L。

3.电荷守恒、电子守恒

例22：在一定条件下，RO₃^n-和F₂可发生如下反应：RO₃^n-+F₂+2OH^-=RO₄^-+2F^-+H₂O从而可知在RO₃^n-中，元素R的化合价是

A. +4      B. +5      C. +6      D. +7

解析：设元素R在RO₃^n-中的化合价为x。

法一：据电荷守恒：n+1×2=1+2×1，n=1。则x-2×3=-1，x=5。

法二：据电子守恒：(7-x)×1=[0-(-1)]×2，x=5。 

4.元素守恒、电子守恒、电荷守恒

一个正确的氧化还原离子方程式的配平，应同时遵循三个守恒关系，即元素守恒、电子守恒和电荷守恒。

例23：配平方程式：[ ]S_x^2-+[ ]BrO₃^-+[ ]OH^-= [ ]SO₄^2-+[ ]Br^-+[ ]H₂O