解含烃混合气体计算的常用八法
时间:2022-08-12 15:11 来源:摘抄于因特网 作者:王兵 点击:次 所属专题: 混合物计算 烃类
版权申明:凡是署名为“化学自习室”,意味着未能联系到原作者,请原作者看到后与我联系(邮箱:79248376@qq.com)!
一、代数法
代数法在化学计算中应用广泛,常用来解决物质的量、质量、体积等问题,特别适用于对混合物中各组份含量的计算。代数法解化学计算题,先根据题目所求设未知数,再根据化学原理或概念,寻找解题的突破口,把计算题中的已知量和未知量结合起来,找出有关数值间量的关系,建立代数方程式或方程组,再求解。此法能使某些复杂的问题简单化,条理化,程序化,使分析的问题思路清晰,计算准确。
例l CH4在一定条件下反应可以生成C2H4、C2H6(水和其它反应产物忽略不计)。取一定量CH4经反应后得到的混合气体,它在标准状况下的密度为0.780 g/L已知反应中CH4消耗20%,计算混合气体中C2H4的体积分数。
解析:设反应前CH4为1 mol,其中x mol转化为C2H4即生成![]() mol C2H4和
mol C2H4和![]() mol C2H6。反应后混合气体的总物质的量=1 mol ×(1-20%)十
mol C2H6。反应后混合气体的总物质的量=1 mol ×(1-20%)十![]() mol+
mol+![]() mol=0.900mol。
mol=0.900mol。
根据密度的概念列代数方程式:
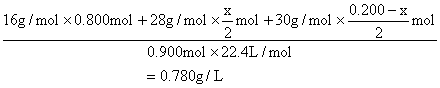
C2H4的体积分数
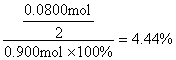 。
。
二、守恒法
化学反应是原子重新组合的过程,原子的种类及数目在反应前后均不发生改变。因此化学反应前反应物的质量总和必然等于反应后生成物的质量总和,即质量守恒。该法在化学计算中应用也很广泛,用此法可以求元素的相对原子质量、相对分子质量、分子式、混合物组成以及进行溶解度、溶液浓度等计算。
此法推广:由甲状态→乙状态(可以是物理变化或化学变化)中,总可找到某一物理量,其值在变化前后不发生变化。利用物理量的不变性列出等式而解题称广义守恒法。在状态改变过程中,其总值可以不变的物理量有:质量、化合价、物质的量、电荷、体积、浓度等。守恒法解题关键是:巧妙地选择两状态中总值不发生改变的物理量,建立关系式,从而简化思路,能使解题达到事半功倍的效果。
例2 把m mol C2H4和n mol H2混合于密闭容器中,在适当的条件下,反应达到平衡时生成p mol C2H6,若将所得平衡混合气体完全燃烧生成CO2和H2O,需要氧气为多少摩尔?
解析:若按化学平衡问题先求出平衡时混合气体各组分各多少摩尔,分别燃烧各需氧气多少摩尔,再求氧气总物质的量,太烦锁。C2H4与H2在整个加成反应过程中C、H原子个数都不变,因而平衡时混合气体耗氧量等于反应前C2H4和H2燃烧耗氧总量。
平衡时混合体燃烧耗氧量=![]() mol。
mol。
三、差量法
任一化学反应:
A 十 B = C + D 差量
a d a—d
x y x—y
存在如下比例关系:
![]() 。
。
化学方程式所反映的各物质的差量存在多种形式,主要是:质量差,物质的量差,压强差等。根据差量法解题公式知,其解题关键是审清题意,依据化学反应列出反应前后有关物质的数量及差量,即a,d及(a-d)再与题目中给定的差量(x-y)组成比例式,求解得答案。
例3 某气态烃与氧气的混合气体在密闭容器中,完全燃烧后容器内压强与燃烧前压强相等,燃烧前后的温度都保持在150℃。该烃不可能是( )。
(A)CH4 (B)C2H4 (C)C3H4 (D)C3H6
解析:设该气态烃分子式为CxHy
则
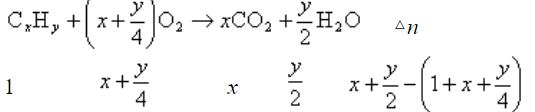
△n=0
即
![]() 。
。
即含4个H原子的烃,100℃以上燃烧前后气体分子数不变,压强不变。选(D)。
同样分析知(1)100℃以上,H原子数小于4的气态烃,燃烧后压强减小:H原子数大于4的气态烃燃烧后,压强增大。(2)100℃以下,因生成水为液态,则所有气态烃燃烧后气体分子数都减小(1+x+![]() ﹥x),压强都减小。
﹥x),压强都减小。
四、中间数值法利用各种物理量的平均值来解化学计算题的方法,称为平均值法。
此法是从求混合气体平均分子量的公式![]() =M1a1%+M2a2%推广而来。它巧用了平均含义,即M1≠M2且均大于零时,存在
=M1a1%+M2a2%推广而来。它巧用了平均含义,即M1≠M2且均大于零时,存在![]() ,只要求出平均值
,只要求出平均值![]() ,就可判断M1,M2的取值范围,该法省去复杂的数学计算过程,从而迅速解出答案。
,就可判断M1,M2的取值范围,该法省去复杂的数学计算过程,从而迅速解出答案。
应当指出上式中M不单指式量,亦可代表相对原子质量、体积、质量、物质的量、摩尔质量及质量分数等。所以应用范围很广,特别适合于分析二元混合物的平均组成。
例4 一种气态烷烃和一种气态烯烃组成的混合物共10克,混合气体的密度是相同状况下氢气的12.5倍,该混合气体通过溴水时,溴水的质量增加8.4克,则该混合气体是由什么组成的?
解析:(1)混合气体平均分子量![]() 。
。
(2)根据中间数值法,确定烷烃是甲烷。
平均分子量等于25的烃有两种情况:两气态烃分子量都等于25,经分析没有这种气态烃;两气态烃中有一种分子量小于25的烃,而分子量小于25的烃只有甲烷,所以两种烃中其中一种必定为CH4。
(3)根据平均分子量求另一种烃设烯烃为CnH2n。
m(烯烃)=8.4g,
m(CH4)=10—8.4=1.6g。

n=2即烯烃是乙烯。
五、十字交叉法
对于具有相同性质(指某些方面)的两种体系,如果用M表示与已知的两个量M1,M2有关的平均值,n1、n2。表示M1,M2对应的分数。
则有:n1M1=n2M2=(n1+n2)![]()
整理得
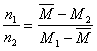
以M为中心可把(1)中五个相关量组合成(斜)十字交叉计算图。
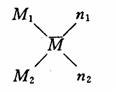
由图知,五个量中知其四,就可求出第五个量;或者知道M1,M2及![]() 就可求两体系的比例,这种运算方法称十字交叉法,十字交叉法简便,敏捷。
就可求两体系的比例,这种运算方法称十字交叉法,十字交叉法简便,敏捷。
十字交叉法一般只适用于两种已知成分组成的混合体系,解题关键往往在于求平均。要搞清十字交叉法中![]() 比值的含义:当以一定质量的混合体系为基准,所得比值为质量比,当以一定物质的量或体积的混合体系为基准,所得比值为物质的量比。
比值的含义:当以一定质量的混合体系为基准,所得比值为质量比,当以一定物质的量或体积的混合体系为基准,所得比值为物质的量比。
十字交叉法应用范围:组分混合体系的总量等于两组的分量之和。溶液混合时一般体积无加和性,对于体积、物质的量浓度不适用。十字交叉法广泛应用于有关同位素、相对原子量、溶质质量、二组分混合物式量分数、化学反应中的物质的量、体积、电子转移数及反应热等方面计算。
例5 有CH4和C2H4混合气体,其密度是同温同压下乙烷的![]() ,求混合气体中CH4的质量分数。
,求混合气体中CH4的质量分数。
解析:相同状态下气体密度比等于分子量之比
![]()
由十字交叉法得:
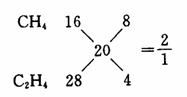
混合气体中CH4的质量分数为![]() 。
。
六、方程式叠加法
叠加法:把各步化学方程式乘以适当的系叠加成一个总的化学方程式,进而找出关系式的方法。
例6 将x mol O2,y mol CH4和z mol Na2O2放入密闭容器中,在150℃条件下用电火花引发,恰好完全反应后,容器内压强为0,通过计算确立x,y和z之间的关系式。
解析:根据反应后气体压强等于0,所以可将以下反应方程式相加,消除气体2CH4+4O2![]() 2CO2十4H2O
2CO2十4H2O
2CO2+2Na2O2=2Na2CO3+O2
2CO2+2Na2O2=8NaOH+2O2
2CH4+O2+6Na2O2=8NaOH+2Na2CO3
所以x:y:z=1:2:6即6x=3y=z。
七、待定系数法
根据题意直接写出方程式,并在反应物及生成物前待以系数,最后找出系数间关系。
例7 丁烷催化裂化时,碳链按两种方式断裂生成两种烷烃和烯烃,若丁烯裂化率为90%,且裂化生成的两种烯烃的质量相等,求裂化后得到的分子量最小气体在混合气体中所占体积分数。
解析:丁烷催化裂化,有如下方程式
C4H10→CH4+C3H6 (1)
C4H10![]() C2H6+C2H4 (2)
C2H6+C2H4 (2)
将(1)(2)合并,系数待配
aC4H10→bCH4+bC3H6+cC2H6+cC2H4
由m(C3H6)=m(C2H4),所以b:c=2:3,
令b=2,则c=3,a=5。
5C4H10![]() 2CH4+2C3H6+3C2H6+3C2H4
2CH4+2C3H6+3C2H6+3C2H4
CH4所占体积分数为![]() =20%。
=20%。
八、讨论法
此法一般适合与其他计算方法一起使用。特点是:由于题中包含不确定因素,必须通过全面的分析,一一列出几种可能性,然后再根据已知条件一一对照几种可能的结论,应用化学概念、化学定律、原理进行分析,逐一将有矛盾的结论淘汰,最后得到正确结论,所以这种解法的关键是进行全面的分析和推断。
例8 1L乙炔和气态烯烃混合物与11LO2混合后点燃,充分反应后,气体的体积为12L,求原1L混合气体中各成分及物质的量比(反应前后均为182℃、1.01×105Pa)。
解析:设混合烃的平均分子式为CxHy
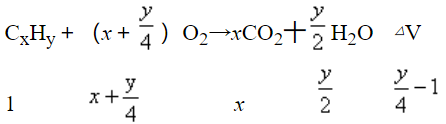
∵△V=0,∴![]() -1=0,y=4
-1=0,y=4
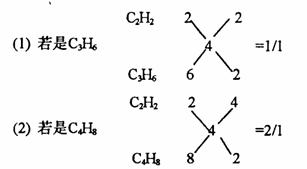
C2H2分子中H原子个数为2,而混合烃平均组成中H原子个数为4。
所以烯烃中H原子个数必大于4,又因为是气态烯烃,碳原子个数必小于4,所以烯烃只能是C3H6或C4H8。
附:(2001年全国高考题第26题 )标准状况下1.68L无色可燃气体在足量氧气中完全燃烧。若将产物通入足量澄清石灰水,得到的白色沉淀质量为15.0g;若用足量碱石灰吸收燃烧产物,增重9.3g。
(1)计算燃烧产物中水的质量。
(2)若原气体是单一气体,通过计算推断它的分子式。
(3)若原气体是两种等物质的量的气体的混合物,其中只有一种是烃,请写出它们的分子式(只要求写出一组)。
答案:H2和C4H6(或CO和C3H8等)。

- 全部评论(0)
