化学自习室移动版

一、十字交叉法的来历

十字交叉法与三角正弦法有着共同的祖先。它们都是由下面的二元一次方程组(求和公式)推导的变式公式得出来的。

求和公式：A＝A₁×w₁＋A₂×w₂ (w₁＋w₂＝1)。

在高低求中类计算中，将A₂理解为两个纯量中的高量，w₂为高量所占的丰度(即物质的量百分含量或气体的体积百分含量)；把A₁理解为低量， w₁为低量所占的丰度；且A₂＞A₁；A为高量及低量组成的混合物的中量。

求和公式有以下五个变式：

① A＝A₁＋(A₂－A₁)×w₂ 

② A＝A₂－(A₂－A₁)×w₁

③ w₁＝

④ w₂＝ 

⑤ ＝

以上变式是化学技巧计算的公式，尤以③、④、⑤用途最大。但由于记忆较难，故改用下列三角正弦图示法，使之变得更为明白、易记和易算。其推导过程如下：

若两个纯量(高量和低量)为一直角三角形的锐角顶点，由它们组成的中量为该直角三角形的直角顶点，三角形的边长为边上两顶点数据之差，那么，可得如下关系：

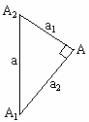
Sin A₁＝＝＝w₁

Sin A₂＝＝＝w₂

＝＝＝

由此可得出三角正弦法则：

高量的丰度就是高量的正弦，低量的丰度就是低量的正弦；高量与低量的比值就是它们所对应的边之比。

若把中量放在十字的中心，高量和低量放在左边的线头上，而把它们的丰度放在右边的线头上，则得到十字交叉法的图示方法。

这种图示与求和公式变式⑤吻合，可理解为求和公式变式⑤的图示法。

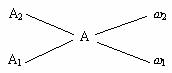
由上推导可知，三角正弦法是求和公式变式④和⑤的图示法。因而它将有两个用途：求比值和丰度。而十字交叉法的用途是求比值，若要求丰度则需另外进行计算。

由此分析还可看出，凡是采用上述求和公式计算的数学和化学计算问题，皆可用十字交叉法和三角正弦法加以快速计算。十字交叉图示法和三角正弦图示法实际上是代替求和公式的一种简捷算法，它特别适合于两总量、两关系的混合物的计算(即2—2型混合物计算)。

二、十字交叉法的应用范围和局限

既然十字交叉图示法和三角正弦图示法的实质一样，只不过一个是伸出去，另一个是缩回来。那末，它们的应用范围和局限都应该一样。它们都可以用来解决以下的有关高低求中的问题。

(1) 同位素(一般求原子数比或原子含量，也可求质量比或质量含量)；

(2) 混合气体(一般求体积比和体积百分含量，或物质的量之比和物质的量百分含量；也可求质量比或质量含量)；

(3) N₂及氮氧化物的混合物；

(4) 气体混合物燃烧；

(5) 平衡混合物；

(6) 反应热；

(7) 固体混合物反应(既可求物质的量比或物质的量百分含量，也可以求质量比或质量百分含量)；

(8) 化肥混合物(只能求质量比或质量百分含量)；

(9) 溶液混合(只能求质量比或质量百分含量)。

例1：铜有两种天然同位素和，铜的相对原子质量为63.5，估算的百分含量约是(MCE86.二.5.)  ( E )

A. 20% B. 25% C. 50% D. 66.7% E. 75%

解析：这种题的常规解法有二：

解法一：设两个未知数，解二元一次方程组。

设和的百分含量分别为x%和y%，可得：

x%＋y%＝1

63x%＋65y%＝63.5

解得：x%＝75%， y%＝25%。故应选E。

解法二：设一个未知数，解一元一次方程式。

设的百分含量为x%，则的百分含量为1－x%，可得：

63x%＋65(1－x%) ＝63.5，

x%＝75%。故应选E。

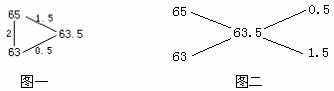
若用三解正弦图示如图一所示，的正弦即为其百分含量，即%＝×100%＝75%。若用十字交叉图示如图二所示，与原子个数比为0.5∶1.5，%＝×100%＝75%。

由上所述，好象十字交叉法和三角正弦法是一种解题方法，但其实它们只是解法一中的二元一次方程组或解法二的一元一次方程式(两者等效)的一种图示简捷算法而已。这可由下面例题的解法中看出。

例2：CH₄在一定条件下催化氧化可以生成C₂H₄、C₂H₆(水和其它产物忽略不计)。取一定量CH₄经催化氧化后得到一种混合气体，它在标准状况下的密度为0.780 g / L。已知反应中CH₄消耗了20.0%，计算混合气体中C₂H₄的体积百分含量。(本题计算过程中保持3位有效数字) (MCE95.)

解法一：设反应前CH₄为1 mol，其中有x mol 转化成C₂H₄，即生成 mol C₂H₄和mol C₂H₆。

反应后混合气体的总物质的量 ＝ 0.800 mol＋0.200 mol× ＝ 0.900 mol

＝ 0.780 g / L

解得 x ＝ 0.0800 mol

C₂H₄的体积百分含量 ＝×100% ＝ 4.44%

解法二：设反应后所得混合气体的相对平均摩尔质量为，反应生成的C₂H₄和C₂H₆两者(C₂Hx )的相对平均摩尔质量为，

＝ 0.780 g / L×22.4 mol / L ＝ 17.472 g / mol

CH₄ ————C₂Hx

0.2 0.1

16×0.8＋0.1×＝17.472 ①

＝29.248

(注：①式可用十字交叉图示和三角正弦图示来计算，如图三和图四。

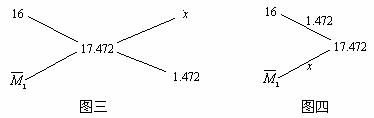
， x ＝ 11.776， ＝ 29.248)

设C₂H₄和C₂H₆在C₂Hx中的物质的量分数分别为y₁和y₂，则可得：28×y₁＋30×y₂＝29.248 ②

＝＝

(注：②式可用十字交叉图示和三角正弦图示来计算，如图五和图六。

　＝＝)

CH₄∶C₂H₄∶C₂H₆ ＝ 0.8∶×5∶×3 ＝ 64∶5∶3

C₂H₄% ＝×100% ＝ 4.17%

由上述分析可知，凡是用以上两种方法能解的二元混合物(涉及高、中、低三种量)的计算问题都可用十字交叉图示法和三角正弦图示法解出，因此，十字交叉法和三角正弦法只是代替上述两种算法的一种图示简捷算法，是一种数学模式；它们只不过比具体解二元一次方程组来得简捷方便而已。

因此，在正式考试解答这类题时，只须在试卷上写出对应的二元一次方程组或一元一次方程式，而在草稿上用十字交叉法或三角正弦法很快解出，将其结果写在答卷上。

正如在应用三角正弦法一样，在应用十字交叉法时要注意的是，有些题既可以求物质的量(或气体体积)比或物质的量(或气体体积)百分含量，又可以求质量比或质量百分含量。对于这种情况，必须弄清怎样使用这两种图示法。通过下面例题的分析和求解能帮助我们很好地认识这两种图示法的使用方法和局限。

(MCE91·27)实验测得乙烯与氧气混合气体的密度是氢气的14.5倍，可知其中乙烯的质量百分比为      (C)

A. 25.0% B. 26.6% C. 72.4% D. 75.0%

解析：由混合气体对氢气的相对密度可求得其平均相对分子质量为29，不少学生就用十字交叉法来解此题：

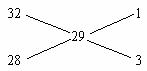
由此可得乙烯的质量百分比为：×100%＝75%。显然，这是错的，因为本题的正确答案是C而不是D。

为什么会出现这种结果，这是因为你实际上是假设了乙烯和氧气的分子数是1个分子(或物质的量是1 mol)，故乙烯和氧气采用的是相对分子质量(或摩尔质量)，画的是质量(即相对分子质量)十字交叉，即本题的前提条件是两种纯量为等分子数(或等物质的量)，只不过表现出来是摩尔质量的数字而已。由于假设的是等分子数(或等物质的量)，因而求得的当然是分子数(或物质的量)的百分含量。当然，由分子个数百分含量也可找到正确答案，这是由于乙烯的相对分子质量比氧气稍小，故乙烯的质量分数稍小于75%，故应选C。只不过不少的学生不知道这样算出来的结果不是质量百分含量，更不会意识到用此结果来寻求正确答案。

对于这种问题，能不能直接用十字交叉法来求质量比或质量分数呢？通过以上分析的思考，使我想到了假设等质量可能会得出正确的结果。这都可以从许多题中得到证实。如果本题要用十字交叉法直接算乙烯的质量分数，则须假设三种量为等质量。若假设等质量为224 g，则氧气的物质的量为7 mol，乙烯为8 mol，混合气体为7.724 mol，画出三者物质的量的十字交叉如下：

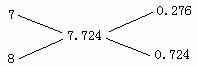
即可得出混合气中乙烯的质量分数是，故应选C。

由此得出的结论是：若要用十字交叉法来求物质的量的关系，须假设两纯量和中量为等物质的量(对于气体也可以设等体积)，找出对应的质量(若设1 mol，则为各物质的摩尔质量，数值就是相对分子质量)，画质量关系的十字交叉图示求解；若要用十字交叉法来求质量的关系，则须假设两纯量和中量为等质量，找出对应的物质的量(对于气体也可以是体积)，然后画物质的量(或体积)十字交叉图示求解。